If the sets A and B are defined are defined as A={(x,y):y=ex,x∈R},B={(x,y):y=x,x∈R}then
B⊂A
A⊂B
A∩B=ϕ
A∪B
The correct Answer is:B
To solve the problem, we need to analyze the sets A and B defined as follows:
- Set A: A={(x,y):y=ex,x∈R}
- Set B: B={(x,y):y=x,x∈R}
1. Understanding Set A:
- The set A represents all points (x,y) where y is equal to ex. This is the exponential function which is always positive for all real numbers x. The graph of this function starts from the point (0,1) and increases rapidly as x increases.
2. Understanding Set B:
- The set B represents all points (x,y) where y is equal to x. This is a straight line that passes through the origin (0, 0) and has a slope of 1.
3. Graphing the Functions:
- To visualize the relationship between the two sets, we can sketch the graphs of both functions:
- The graph of y=ex is an upward-curving exponential function that never touches or crosses the x-axis.
- The graph of y=x is a straight line that passes through the origin and continues indefinitely in both directions.
4. Finding Points of Intersection:
- We need to find if there are any points where the two graphs intersect, which means we need to solve the equation:
ex=x
- To analyze this, we can consider the behavior of both functions:
- For x<0, ex is positive and x is negative, so they cannot intersect.
- For x=0, e0=1 and 0=0, so they do not intersect at this point.
- For x>0, ex grows much faster than x, indicating that they will not intersect.
5. Conclusion:
- Since there are no points (x,y) that satisfy both conditions simultaneously, we conclude that the intersection of sets A and B is empty:
A∩B=∅
Final Answer:
The relation between sets A and B is:
A∩B=∅
- Set B: B={(x,y):y=x,x∈R}
- The set A represents all points (x,y) where y is equal to ex. This is the exponential function which is always positive for all real numbers x. The graph of this function starts from the point (0,1) and increases rapidly as x increases.
- The set B represents all points (x,y) where y is equal to x. This is a straight line that passes through the origin (0, 0) and has a slope of 1.
- To visualize the relationship between the two sets, we can sketch the graphs of both functions:
- The graph of y=ex is an upward-curving exponential function that never touches or crosses the x-axis.
- The graph of y=x is a straight line that passes through the origin and continues indefinitely in both directions.
- We need to find if there are any points where the two graphs intersect, which means we need to solve the equation:
ex=x
- To analyze this, we can consider the behavior of both functions:
- For x<0, ex is positive and x is negative, so they cannot intersect.
- For x=0, e0=1 and 0=0, so they do not intersect at this point.
- For x>0, ex grows much faster than x, indicating that they will not intersect.
- Since there are no points (x,y) that satisfy both conditions simultaneously, we conclude that the intersection of sets A and B is empty:
A∩B=∅
The relation between sets A and B is:
A∩B=∅
Topper's Solved these Questions
- SETS, RELATIONS AND FUNCTIONS Book:ARIHANT MATHS ENGLISHChapter:SETS, RELATIONS AND FUNCTIONS Exercise:Exercise (More Than One Correct Option Type Questions)
Explore 3 Videos
- SETS, RELATIONS AND FUNCTIONS Book:ARIHANT MATHS ENGLISHChapter:SETS, RELATIONS AND FUNCTIONS Exercise:Exercise (Passage Based Questions)
Explore 6 Videos
- SETS, RELATIONS AND FUNCTIONS Book:ARIHANT MATHS ENGLISHChapter:SETS, RELATIONS AND FUNCTIONS Exercise:Exercise For Session 3
Explore 10 Videos
- SEQUENCES AND SERIESBook:ARIHANT MATHS ENGLISHChapter:SEQUENCES AND SERIESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 38 Videos
- THE STRAIGHT LINESBook:ARIHANT MATHS ENGLISHChapter:THE STRAIGHT LINESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 17 Videos
Similar Questions
If set A and B are defined as
A={(x,y)∣y=1x,0≠x∈R},B={(x,y)∣y=−x,x∈R,}. Then
View SolutionIf set A and B are defined as
A={(x,y)∣y=1x,0≠x∈R},B={(x,y)∣y=−x,x∈R,}. Then (a) A ∩ B = A (b)A ∩ B = B (c)A ∩ B = ϕ (d)A ∪ B = A
View SolutionifA={(x,y):x2+y2=4,x,y∈R}and
B={(x,y):Y=|x|,x,y∈R} then
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
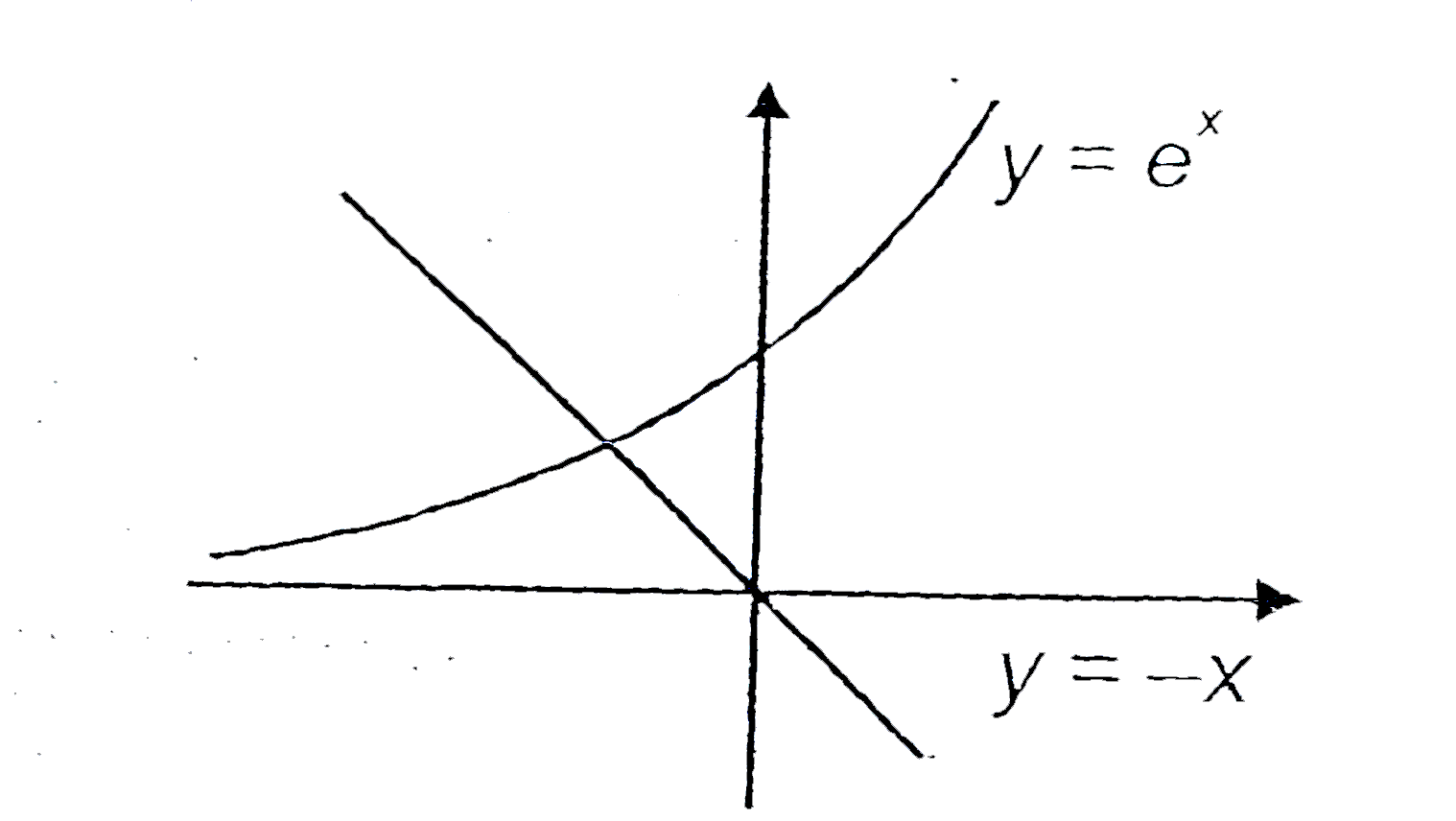
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):x2+y2≤2,x,y∈R}
B={{x,y):y≥x2,x,y∈R}
View SolutionA point chanrge of magnitude q=4.5nC is moving with speed v=3.6×107ms−1 parallel to the x-axis along the line y=3m. Find the magnetic field at the origin produced by this charge when the charge is at the point x=−4m, y=3m, as shown in Fig.

View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
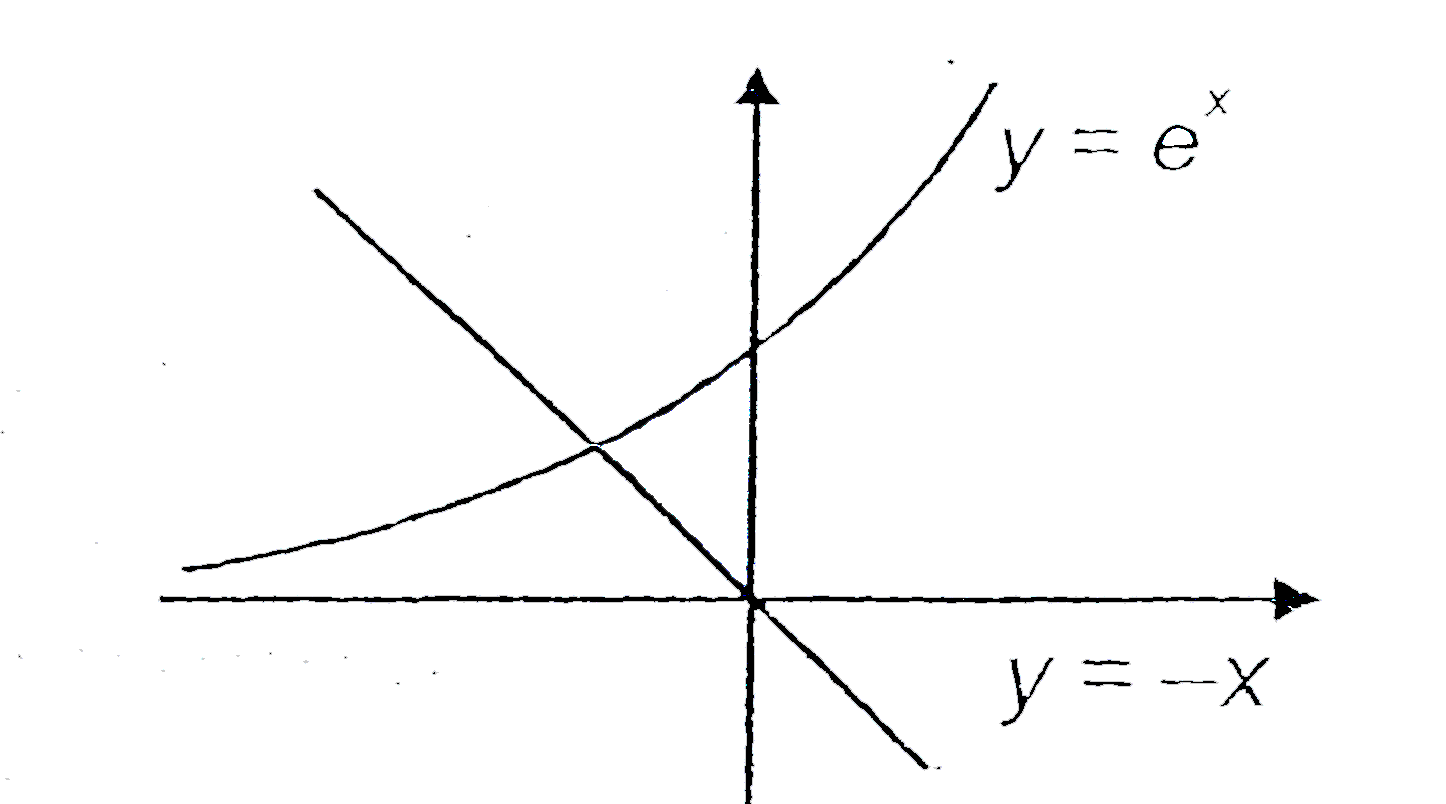
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A:{(x,y):y=√4−x2,x∈[−2,2]}
B={(x,y):y=|x|,x∈R}
Then n(A∩B)
View SolutionifA={(x,y):y=4x,x≠0}and
B={(x,y):x2+y2=8,x,y∈R},then
View SolutionWhich of the following are function: {(x,y):y2=x,x,y∈R} b. {(x,y):y=|x|,x,y∈R} c. {(x,y):x2+y2=1,x,y∈R} d. {(x,y):x2−y2=1,x,y∈R}
View SolutionIf A={(x, y):y=ex, x∈R}and B={(x,y):y=e−x, x∈R} , then write A∩B.
View SolutionifA={(x,y):x2+y2=4,x,y∈R}and
B={(x,y):x2+y2=9,x,y∈R},then
View Solution

