If set A and B are defined as
A={(x,y)∣y=1x,0≠x∈R},B={(x,y)∣y=−x,x∈R,}. Then
A∩B=A
A∪B=B
A∪B=ϕ
A∪B−A
The correct Answer is:C
To solve the problem, we need to analyze the sets A and B and determine their intersection and union.
Step 1: Define the sets A and B
- Set A is defined as A={(x,y)|y=1x,x≠0,x∈R}.
- Set B is defined as B={(x,y)|y=−x,x∈R}.
Step 2: Find the intersection of sets A and B
To find the intersection A∩B, we need to find the points that satisfy both conditions:
1. From set A: y=1x
2. From set B: y=−x
Setting these equal to each other gives:
1x=−x
Step 3: Solve the equation
Multiplying both sides by x (keeping in mind x≠0):
1=−x2
Rearranging this gives:
x2=−1
Step 4: Analyze the result
The equation x2=−1 has no real solutions because the square of a real number cannot be negative. Therefore, there are no points that belong to both sets A and B.
Step 5: Conclusion about the intersection
Since there are no common points, we conclude that:
A∩B=∅
Step 6: Analyze the union of sets A and B
The union A∪B consists of all points that are in either set A or set B. Since there are no points in the intersection, the union is simply the combination of both sets.
Final Result
- A∩B=∅
- A∪B contains all points from both sets.
- Set A is defined as A={(x,y)|y=1x,x≠0,x∈R}.
- Set B is defined as B={(x,y)|y=−x,x∈R}.
To find the intersection A∩B, we need to find the points that satisfy both conditions:
1. From set A: y=1x
2. From set B: y=−x
1x=−x
Multiplying both sides by x (keeping in mind x≠0):
1=−x2
Rearranging this gives:
x2=−1
The equation x2=−1 has no real solutions because the square of a real number cannot be negative. Therefore, there are no points that belong to both sets A and B.
Since there are no common points, we conclude that:
A∩B=∅
The union A∪B consists of all points that are in either set A or set B. Since there are no points in the intersection, the union is simply the combination of both sets.
- A∩B=∅
- A∪B contains all points from both sets.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Archives1videos
SET THEORY AND REAL NUMBER SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - SET THEORY AND REAL NUMBER SYSTEM EXERCISE - Concept Application Exercise 1.512videos
SET THEORY AND REAL NUMBER SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
- BOOK - CENGAGE ENGLISHCHAPTER - SOLUTIONS AND PROPERTIES OF TRIANGLE EXERCISE - Comprehension Type6videos
SOLUTIONS AND PROPERTIES OF TRIANGLE
Similar Questions
If the sets A and B are defined are defined as A={(x,y):y=ex,x∈R},B={(x,y):y=x,x∈R}then
View SolutionifA={(x,y):x2+y2=4,x,y∈R}and
B={(x,y):Y=|x|,x,y∈R} thenView SolutionA point chanrge of magnitude q=4.5nC is moving with speed v=3.6×107ms−1 parallel to the x-axis along the line y=3m. Find the magnetic field at the origin produced by this charge when the charge is at the point x=−4m, y=3m, as shown in Fig.
 View Solution
View SolutionIf A={(x, y):y=1x, 0≠x∈R}and B={(x,y):y=−x, x∈R} , then write A∩B.
View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
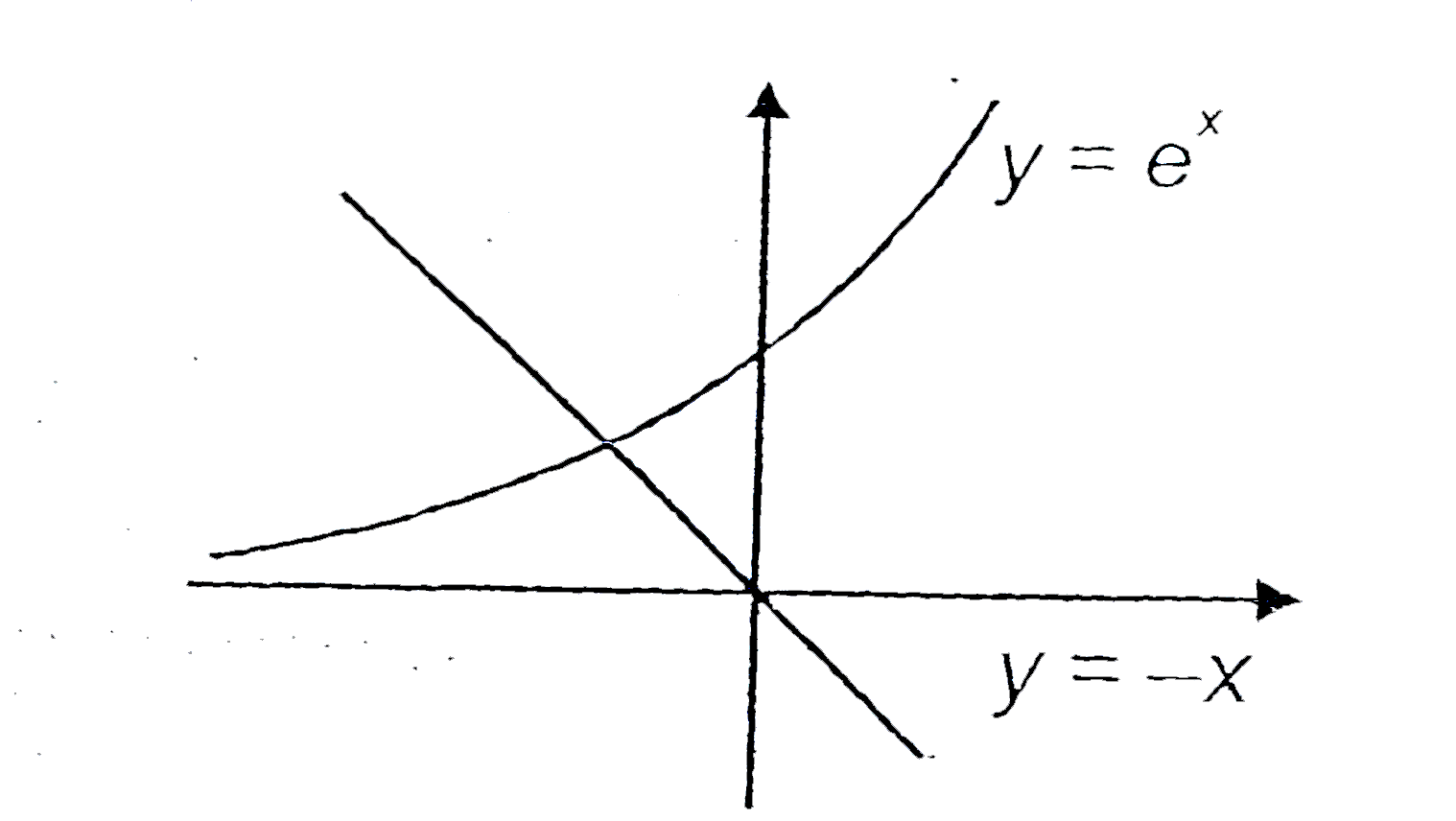
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A={(x,y):x2+y2≤2,x,y∈R}
B={{x,y):y≥x2,x,y∈R}View SolutionIn some question of sets, we have to make the use of graphs
For example
A={(x,y):y=ex,x∈R}
B={{x,y}:y=−x.x∈R}
Find n(A∩B)
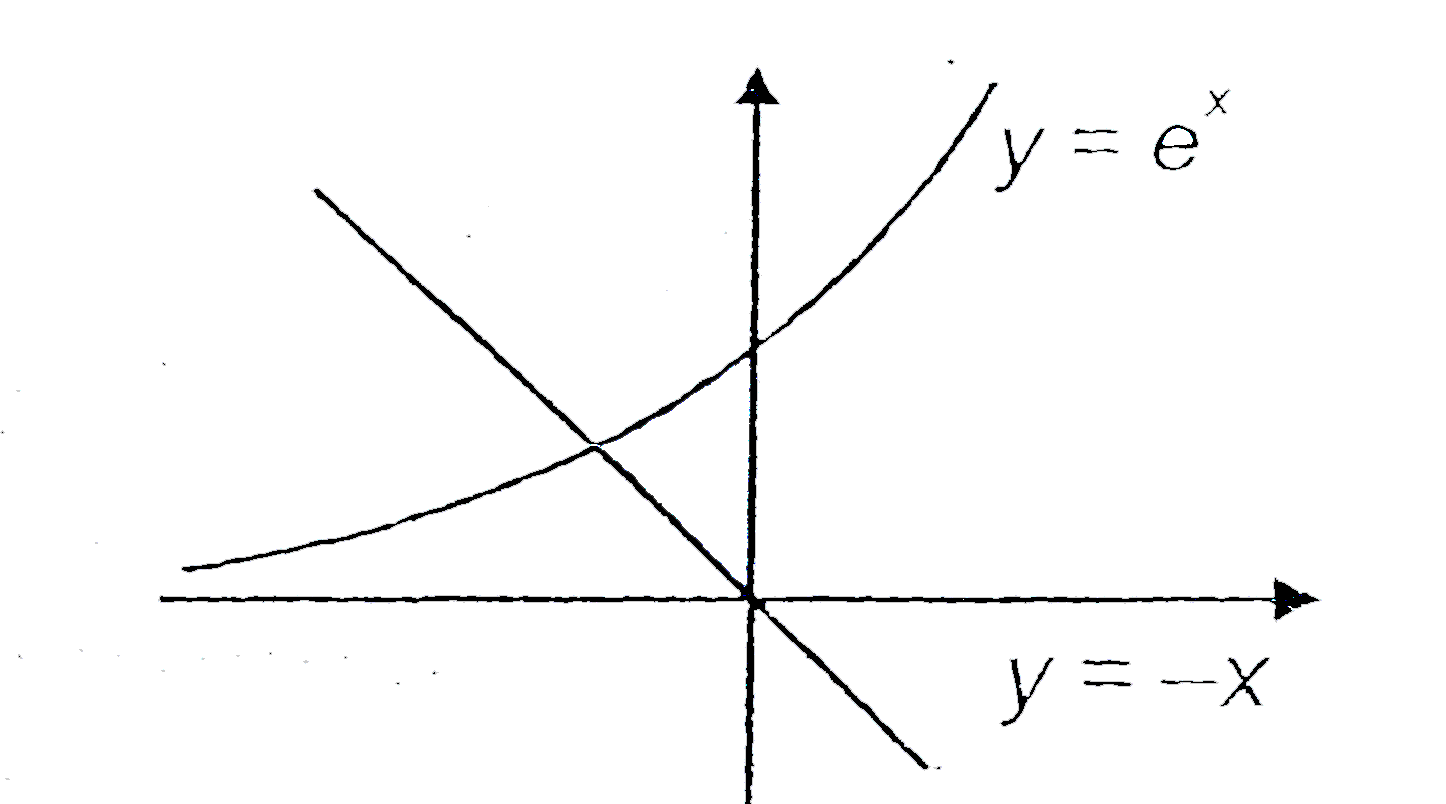
It is clear that y=exandy=−x intersect at one pont. Hence n(A∩B)=1
A:{(x,y):y=√4−x2,x∈[−2,2]}
B={(x,y):y=|x|,x∈R}
Then n(A∩B)View SolutionifA={(x,y):y=4x,x≠0}and
B={(x,y):x2+y2=8,x,y∈R},thenView SolutionLet A = {2, 3, 4}, B ={3, 4, 5} be two sets and a relation R is defined from A to B is such that R ={(x, y) : x divides y, x∈A,y∈B} then domain of R is
View SolutionIf A={(x, y):y=ex, x∈R}and B={(x,y):y=e−x, x∈R} , then write A∩B.
View SolutionLet N be the set of natural numbers and the relation R be defined on N such that R={(x,y):y=2x,x,y∈N}.What is the domain, codomain and range of R? Is this relation a function?
View Solution
