Which one of the following is not true?
A−B⊆A
B'−A'⊆A
A⊆A−B
A∩B'⊆A
The correct Answer is:C
To determine which statement is not true among the given options, we will analyze each statement step by step.
Step 1: Understand the Sets
Let’s define two sets:
- Let A be a set of elements.
- Let B be another set of elements.
Step 2: Analyze Each Statement
1. Statement 1: A−B⊆A
- The expression A−B represents the set of elements that are in A but not in B.
- Since all elements of A−B are derived from A, it follows that A−B is indeed a subset of A.
- Conclusion: This statement is true.
2. Statement 2: B′−A′⊆A
- Here, B′ (or Bc) represents the complement of set B, which includes all elements not in B.
- The expression B′−A′ represents the elements that are in B′ but not in A′.
- Since A′ includes elements not in A, removing A′ from B′ will still leave us with elements that are not in B and could potentially be in A.
- Therefore, B′−A′ can still include elements that are not in A.
- Conclusion: This statement is not necessarily true.
3. Statement 3: A⊆A−B
- This statement claims that A is a subset of A−B.
- However, A−B consists of elements in A that are not in B. Therefore, if an element is in B, it cannot be in A−B.
- This means that A cannot be a subset of A−B since there could be elements in A that are also in B.
- Conclusion: This statement is false.
4. Statement 4: A∩B′⊆A
- The expression A∩B′ represents the intersection of set A with the complement of B.
- This means we are looking at elements that are in A and not in B.
- Since all elements in A∩B′ are also in A, this statement is true.
- Conclusion: This statement is true.
Final Conclusion
From the analysis:
- Statement 1 is true.
- Statement 2 is not necessarily true.
- Statement 3 is false.
- Statement 4 is true.
Thus, the statement that is not true is Statement 3: A⊆A−B.
Let’s define two sets:
- Let A be a set of elements.
- Let B be another set of elements.
- The expression A−B represents the set of elements that are in A but not in B.
- Since all elements of A−B are derived from A, it follows that A−B is indeed a subset of A.
- Conclusion: This statement is true.
- Here, B′ (or Bc) represents the complement of set B, which includes all elements not in B.
- The expression B′−A′ represents the elements that are in B′ but not in A′.
- Since A′ includes elements not in A, removing A′ from B′ will still leave us with elements that are not in B and could potentially be in A.
- Therefore, B′−A′ can still include elements that are not in A.
- Conclusion: This statement is not necessarily true.
- This statement claims that A is a subset of A−B.
- However, A−B consists of elements in A that are not in B. Therefore, if an element is in B, it cannot be in A−B.
- This means that A cannot be a subset of A−B since there could be elements in A that are also in B.
- Conclusion: This statement is false.
- The expression A∩B′ represents the intersection of set A with the complement of B.
- This means we are looking at elements that are in A and not in B.
- Since all elements in A∩B′ are also in A, this statement is true.
- Conclusion: This statement is true.
From the analysis:
- Statement 1 is true.
- Statement 2 is not necessarily true.
- Statement 3 is false.
- Statement 4 is true.
Topper's Solved these Questions
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise (More Than One Correct Option Type Questions)
3 Videos
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise (Passage Based Questions)
6 Videos
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise For Session 3
10 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
- THE STRAIGHT LINESBOOK - ARIHANT MATHS ENGLISHCHAPTER - THE STRAIGHT LINESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
17 Videos
Similar Questions
Knowledge Check
In the figure, ABCD is a parallelogram. Which one of the following is true?
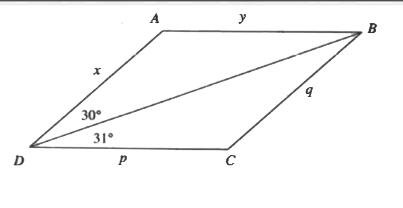 Ax<yBx>qCx>pDy>p
Ax<yBx>qCx>pDy>pWhich one of the following is the true regarding the triangle shown in figure?
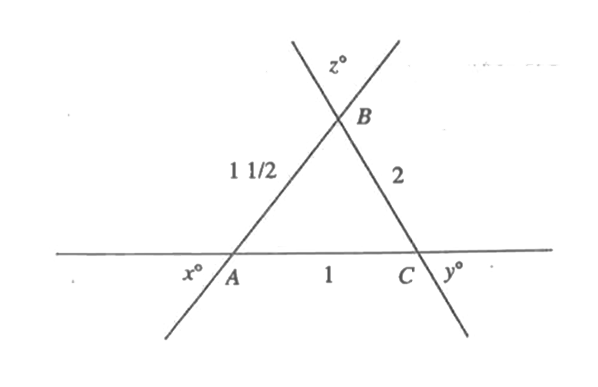 Ax>y>zBx<y<zCx=y=zD2x=3y/2=z
Ax>y>zBx<y<zCx=y=zD2x=3y/2=zIf 9/100 of x is 9, then which one of the following is true?
A25 percent of x is 25B1/4 of x is 0.25Cx is 120% of 80Dx is 9 percent of 90
In a ΔABC ,which one of the following is true?
View SolutionWhich one of the following is the true description about an animal concerned
View SolutionWhich one of the following is a true match
View SolutionWhich one of the following is a true fish ?
View SolutionIf the point (a,b) is in Quadrant II and |a|−|b|>0, then which one of the following is true?
View Solution
