If both the roots of the quadratic equation $x^{2} - 2 k x + k^{2} + k - 5 = 0$ are less than 5, then k lies in the interval.

A

$(- \infty, 4)$

B

$[4, 5]$

C

$(5, 6)$

D

$(6, \infty)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Let $f (x) = x^{2} - 2 k x + k^{2} + k$ then $α$
Consider the following cases:

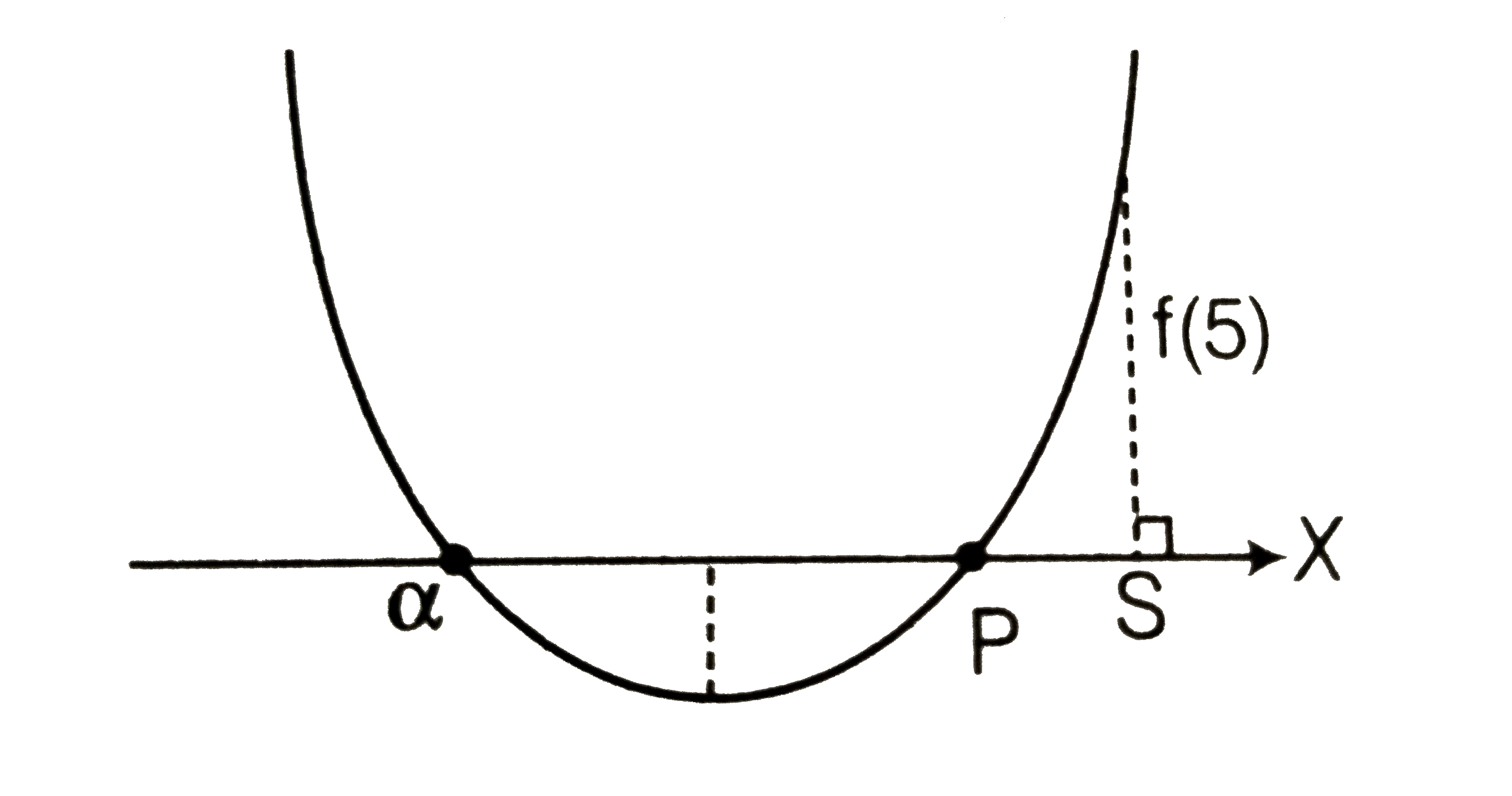
Case I $D \geq 0$
$\Rightarrow 4 k^{2} - 4.1 (i k^{2} + k - 5) \geq 0$
$\Rightarrow - 4 (k - 5) \geq 0$
$\Rightarrow k - 5 \leq 0$
$\Rightarrow k \leq 5$ or $k ε (- \infty, 5]$
Case II x-Coordinate of vertex $x < 5$
$\Rightarrow \frac{2 k}{2} < 5$
$\Rightarrow k < 5$ or $k ε (- \infty, 5)$
Case III $f (5) > 0$
$\Rightarrow 2 - 10 k + k^{2} + k - 5 > 0$
$\Rightarrow k^{2} - 9 k + 20 > 0$
$\Rightarrow (k - 4) (k - 5) > 0$ or $k ε (- \infty, 4) \cup (5, \infty)$
Combining all cases, we get
$k ε (- \infty, 4)$

Updated on:21/07/2023

|

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

If the roots of the quadratic equation $x^{2} + 4 x + k = 0$ are real, then the value of k is:
A $k \geq 4$
B $k > 4$
C $k < 4$
D $k \leq 4$
If the roots of the quadratic equation $2 k x^{2} + (2 a + b) x - a b = 0$ are (-2, a), the value of k is:
A $- 1$
B $- 2$
C1
D2

ARIHANT MATHS ENGLISH-THEORY OF EQUATIONS-Exercise (Questions Asked In Previous 13 Years Exam)

Home
Ask Doubt
Profile