Suppose the cubic $x^{3} - p x + q$ has three distinct real roots, where $p > 0$ and $q > 0$ . Then find the max and min points .

A

a) The cubic has minima at $(- \sqrt{\frac{p}{3}})$ and maxima at $\sqrt{\frac{p}{3}}$

B

The cubic has minima at both $\sqrt{\frac{p}{3}}$ and $(- \sqrt{\frac{p}{3}})$

C

The cubic has maxima at both $\sqrt{\frac{p}{3}}$ and $(- \sqrt{\frac{p}{3}})$

D

The cubic has minima at $\sqrt{\frac{p}{3}}$ and maxima at $(- \sqrt{\frac{p}{3}})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Let $f (x) = x^{3} - p x + q$
$∴ f' (x) = 3 x^{2} - p$
$\Rightarrow f'' (x) = 6 x$

For maxima or minima $f' (x) = 0$
$∴ x = \pm \sqrt{\frac{p}{3}}$
$\Rightarrow f'' (\sqrt{\frac{p}{3}}) = 6 \sqrt{(\frac{p}{3})} > 0$
and $f'' (- \sqrt{\frac{p}{3}} = - 6 \sqrt{\frac{p}{3}} < 0$
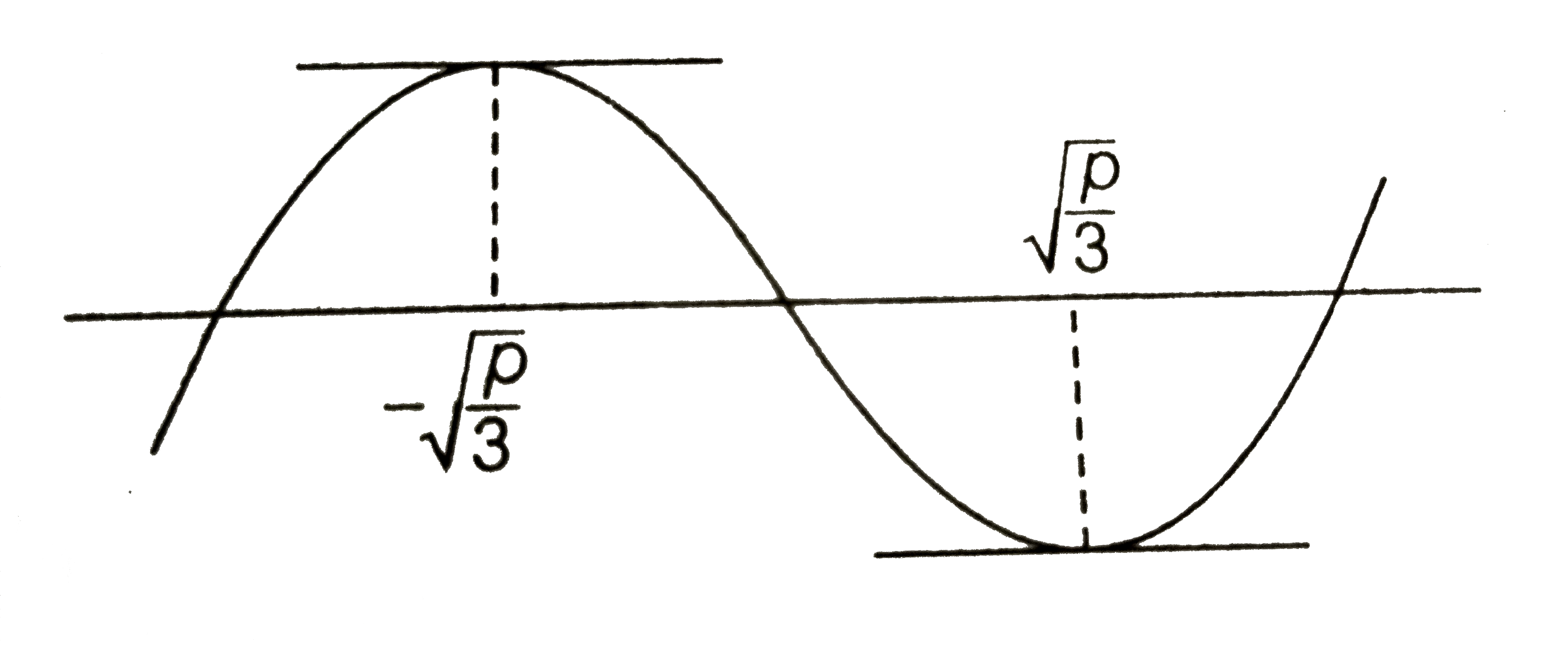
Hence given cubic minima at $x = \sqrt{\frac{p}{3}}$ and maxima at $x = - \sqrt{\frac{p}{3}}$

|

Updated on:21/07/2023

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If the equation $x^{2} + 6 x + p = 0$ has real and distinct roots, then:
A $p < 9$
B $p > 9$
C $p \leq 9$
D $p \geq 9$
Question 2 - Select One
If the equation $3 x^{2} - 6 x + k = 0$ has real and distinct roots, then the value of k is
A $k \leq 3$
B $k = 3$
C $k > 3$
D $k < 3$

ARIHANT MATHS ENGLISH-THEORY OF EQUATIONS-Exercise (Questions Asked In Previous 13 Years Exam)

Home
Ask Doubt
Profile