The refracting angle of a prism is A and refractive index of the material of prism is cot(A/2) . The angle of minimum deviation will be
180 – A
180 – 2A
90 – A
A/2
The correct Answer is:B
To find the angle of minimum deviation (Δ) for a prism with a refracting angle (A) and a refractive index (μ) given as cot(A/2), we can use the formula for the refractive index of a prism:
μ=sin(A+Δmin2)sin(A2)
1. Write down the given information:
- Refracting angle of the prism, A
- Refractive index, μ=cot(A2)
2. Substitute the value of μ into the prism formula:
cot(A2)=sin(A+Δmin2)sin(A2)
3. Rewrite cotangent in terms of sine and cosine:
cot(A2)=cos(A2)sin(A2)
4. Set the two expressions equal:
cos(A2)sin(A2)=sin(A+Δmin2)sin(A2)
5. Cancel sin(A2) from both sides (assuming it is not zero):
cos(A2)=sin(A+Δmin2)
6. Use the identity sin(90∘−x)=cos(x):
sin(90∘−A2)=sin(A+Δmin2)
7. Equate the angles:
90∘−A2=A+Δmin2
8. Multiply through by 2 to eliminate the fraction:
180∘−A=A+Δmin
9. Rearranging gives:
Δmin=180∘−A−A=180∘−2A
10. Final Result:
The angle of minimum deviation is:
Δmin=180∘−2A
- Refracting angle of the prism, A
- Refractive index, μ=cot(A2)
cot(A2)=sin(A+Δmin2)sin(A2)
cot(A2)=cos(A2)sin(A2)
cos(A2)sin(A2)=sin(A+Δmin2)sin(A2)
cos(A2)=sin(A+Δmin2)
sin(90∘−A2)=sin(A+Δmin2)
90∘−A2=A+Δmin2
180∘−A=A+Δmin
Δmin=180∘−A−A=180∘−2A
The angle of minimum deviation is:
Δmin=180∘−2A
Similar Questions
The refracting angle of a prism is A, and refractive index of the material of the prism is cot(A2). The angle of minimum deviation is
View SolutionThe refractive index of the material of prism √3, then the angle of minimum deviation of prism is
View SolutionThe refracting angle of the prism is 60∘ and the refractive index of the material of the prism is √3. Calculate the angle of minimum deviation in degree.
View SolutionA ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A=60∘ and the refractive index of the material of prism is 3^1/2, then the angle of deviation of the ray is

View SolutionWhen light rays are incident on a prism at an angle of 45∘, the minimum deviation is obtained. If refractive index of the material of prism is √2, then the angle of prism will be
View SolutionThe correct relation between the refractive index (μ) of the material of prism (A) and angle of minimum deviation (δ) is
View SolutionA certain prism of refracting angle 60∘ and of refractive index 2 is immersed in a liquid of refractive index √2 then the angle of minimum deviation will be
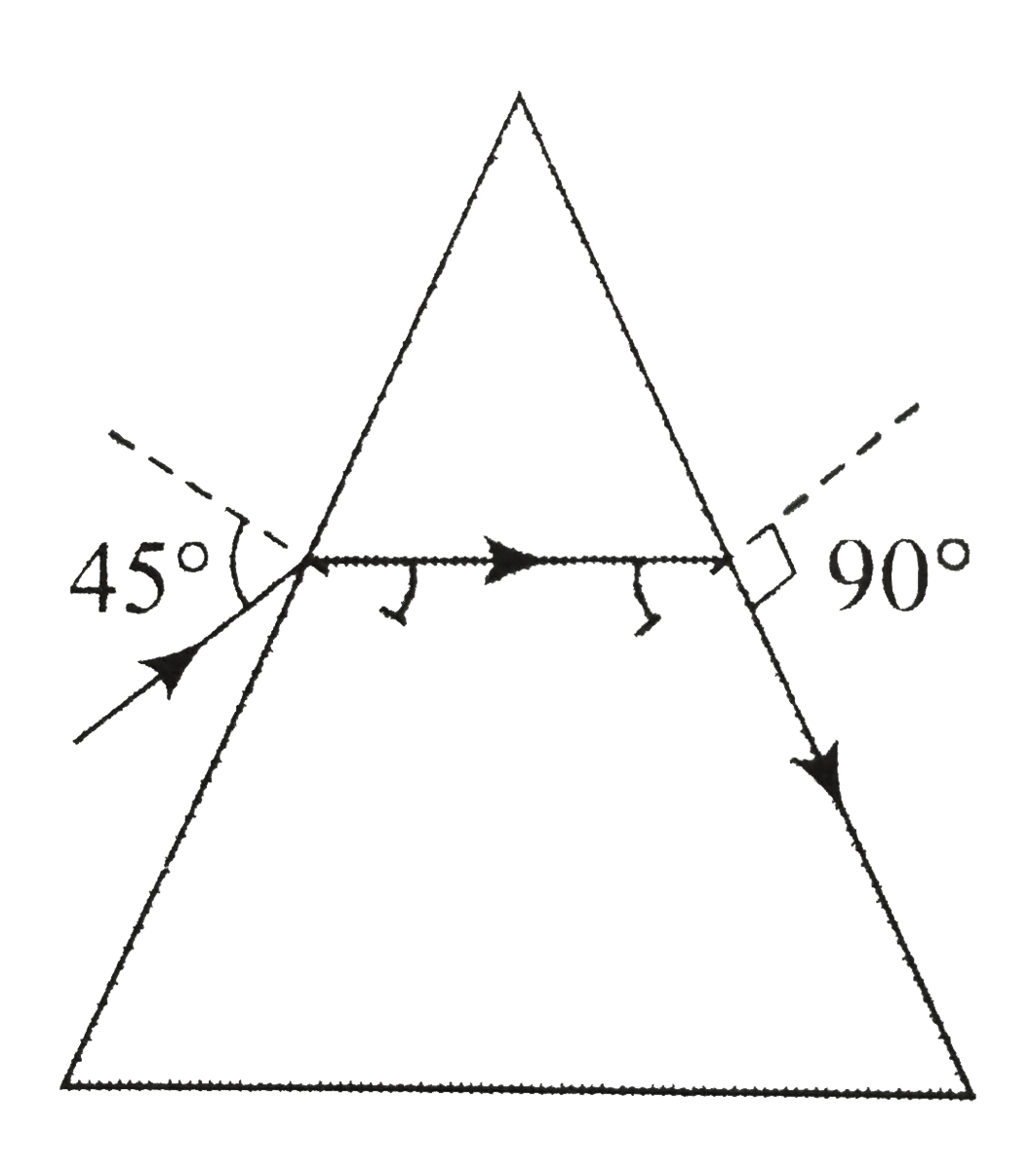
View SolutionIn an isosceles prism of angle 45∘, it is found that when the angle of incidence is same as the prism angle, the emergen ray grazes the emergent surface.
Find the refractive index of the material of the prism. For what angle of incidenc, the angle of deviation will be minimum?
View SolutionA prism is made up of material of refractive index √3. The angle of prism is A. If the angle of minimum deviation is equal to the angle of the prism, then the value of A is
View Solution(a) Plot a graph for angle of deviation as a function of angle of incidence for a triangular prism.
(b) Derive the relation for the refractive index of the prism in terms of the angle of minimum deviation and angle of prism.
View Solution
