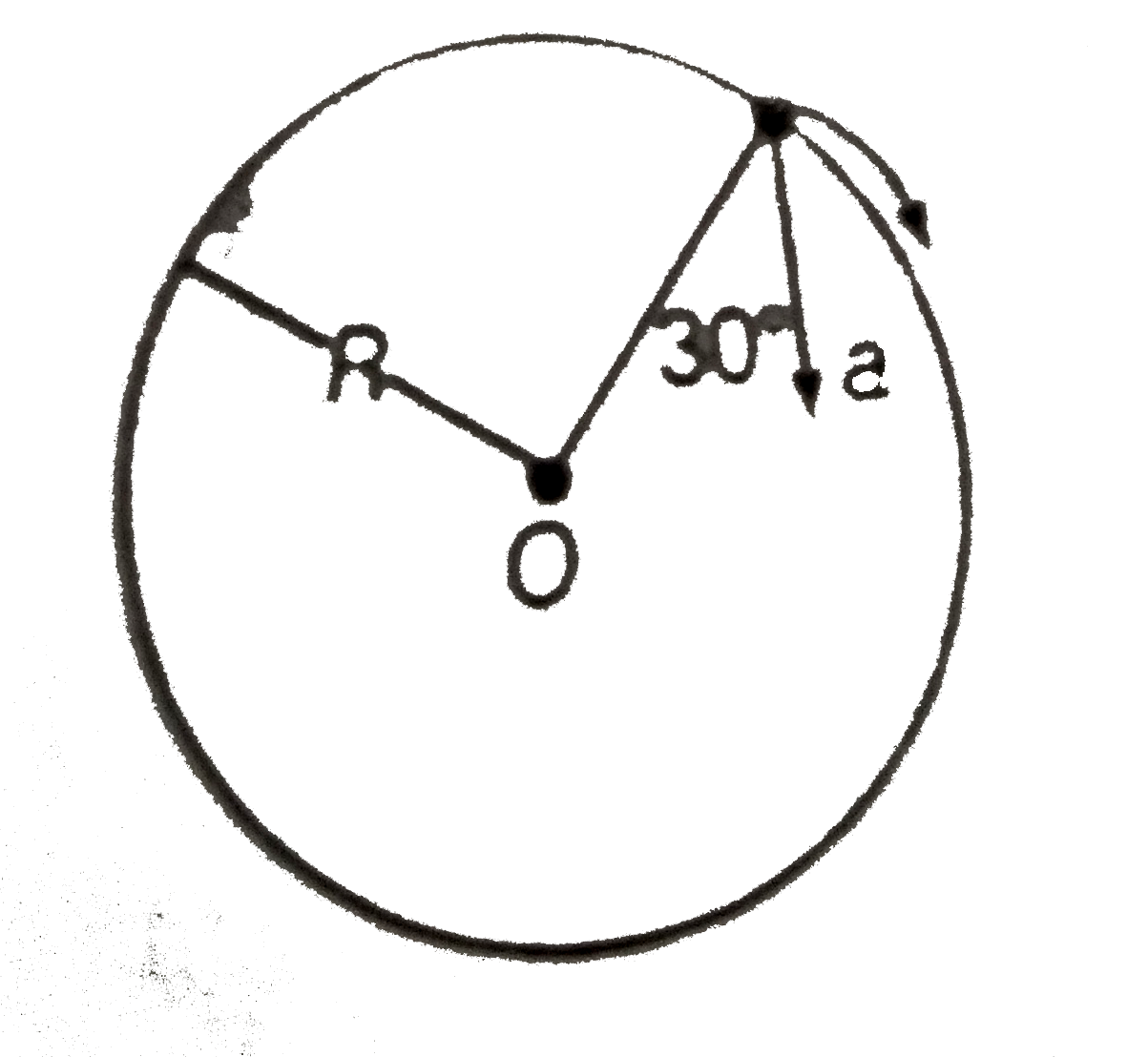
in the given figure, α=15m/s2 represents the total accleration of a particle moving in the clockwise direction on a circle radius R = 2.5m aat a given of time The speed of the particle is
4.5m/s
5.0m/s
5.7m/s
6.2 m/s
The correct Answer is:C
Tanθ=dv/dtV2/R
Tan30∘=1√3=dV/dtV2/R
dVdt=1√3×V2R
a=15=√(dVdt)2+(V2R)2 ltBrgt 15=√43(V2R)2
15=2√3(V2R)=2√3×V22.5⇒V2=15×√3×2.52=32.476=5.7m/s
Similar Questions
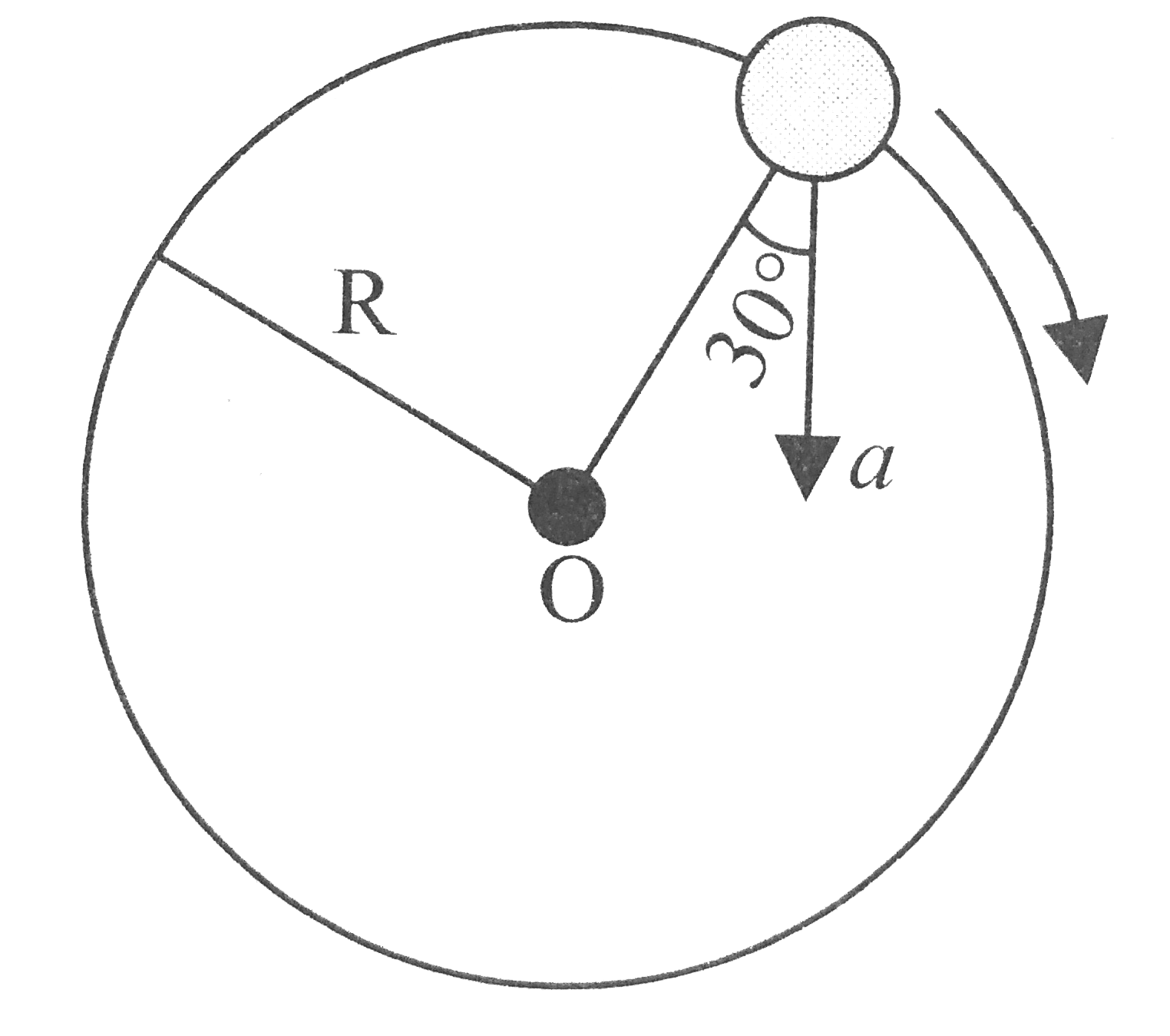
In the given figure, a=15m/s2 represents the total acceleration of a particle moving in the clockwise direction in a circle of radius R=2.5m at a given instant of time. The speed of the particle is.
View SolutionThe figure shows the total acceleration a=32ms−2 of a moving particle moving clockwise in a circle of radius R = 1 m . What are the centripetal acceleration a and speed of the particle at the given instant ?

View SolutionCentripetal acceleration of a particle of mass m moving in a circle of radius r is 4/r2. What is the angular momentum of the particle ?
View SolutionFigur shows the total acceleration and velocity of a particle moving clockwise in a circle of radius 2.5m at a given instant of time. At this instant, find:
(a) the radius acceleration,
(b) the speed of the acceleration,
(c) its tangential acceleration.

View SolutionFigure shows the direction of the total acceleration and velocity of a particle moving clockwise in a circle radius m at an instant of time. Tangential acceleration this instant is 5m/s2. Which of the following statements is not correct?

View SolutionIf a particle moves in a circle of radius of 4m at speed given by v=2t where v is in m/s and t in sec.At t=4s ,net accleration of particle will be:
View SolutionA particle moves in a circle of radius 5 cm with constant speed and time period 0.2πs. The acceleration of the particle is
View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View SolutionA particle of mass m is being circulated on a vertical circle of radius r. If the speed of particle at the highest point be v, then
View SolutionThe co-ordinates of a moving particle at any time t are given by x=ct2andy=bt2The speed of the particle is
View Solution
