Activation energy (Ea) and rate constants (k1 and k2) of a chemical reaction at two different temperatures (T1 and T2) are related by
(a) ln.k2k1=−EaR(1T2−1T1)
(b) ln.k2k1=−EaR(1T2+1T1)
(c) ln.k2k1=EaR(1T1−1T2)
(d) ln.k2k1=−EaR(1T1−1T2)
The correct Answer is:A, C
Ace. To Arrheneis equation
ln.K2K1=EaR[1T1−1T2]
option (1) and (3) are same
Similar Questions
Activation energy (Ea) and rate constants (k1andk2) of a chemical reaction at two different temperature (T1andT2) are related by
View SolutionThe rate constants k1 and k2 of two reactions are in the ratio 2:1. The corresponding energies of acativation of the two reaction will be related by
View Solution
Knowledge Check
Two walls of thickness d1andd2 and thermal conductivites K1andK2 are in contact. In the steady state, if the temperature at the outer surfaces are T1andT2 the temperature at the common wall is
AK1T1d2+K2T2d1K1d2+K2d1BK1T1+K2T2d2+d1C(K1d1+K2d2T1+T2)T1T2DK1T1d1+K2T2d2K1d1+K2d2
A colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.
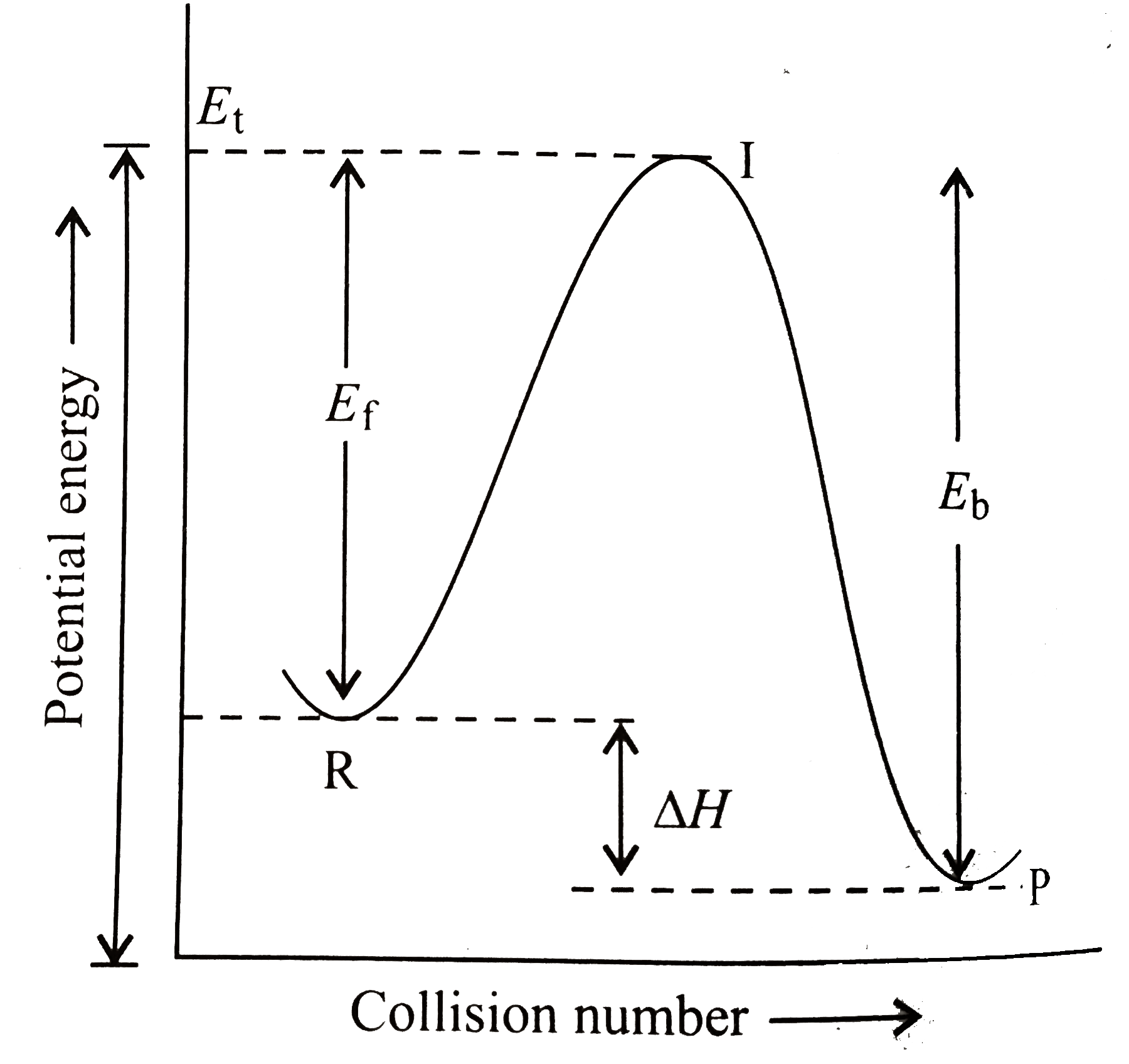
Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
For two reactions, activation energies are Ea1 and Ea2, rate constant are k1 and k2 at the same temperature. If k1>k2, then
View SolutionTwo reaction : X→ Products and Y→ Products have rate constants k1 and k2 at temperature T and activation energies E1 and E2, respectively. If k1>k2 and E1<E2 (assuming that the Arrhenius factor is same for both the Products), then
(I) On increaisng the temperature, increase in k2 will be greater than increaisng in k1.
(II) On increaisng the temperature, increase in k1 will be greater than increase in k2.
(III) At higher temperature, k1 will be closer to k2.
(IV) At lower temperature, k1<k2
View SolutionCondider two rods of same length and different specific heats (s1,s2), thermal conductivities (K1,K2) and areas of cross-section (A1,A2) and both having temperatures (T1,T2) at their ends. If their rate of loss of heat due to conduction are equal, then
View SolutionVariation of equilibrium constan K with temperature is given by van't Hoff equation
InK=ΔrS∘R−ΔrH∘RT
for this equation, (ΔrH∘) can be evaluated if equilibrium constants K1 and K2 at two temperature T1 and T2 are known.
log(K2K1)=ΔrH∘2.303R[1T1−1T2]
For an isomerization X(g)⇔Y(g) the temperature dependency of equilibrium constant is given by :
lnK=2−1000T
The value of ΔrS∘ at 300K is :
View SolutionVariation of equilibrium constan K with temperature is given by van't Hoff equation
InK=ΔrS∘R−ΔrH∘RT
for this equation, (ΔrH∘) can be evaluated if equilibrium constans K1 and K2 at two temperature T1 and T2 are known.
log(K2K1)=ΔrH∘2.303R[1T1−1T2]
Select the correct statement :
View SolutionA mass is suspended separately by two springs of spring constants k1 and k2 in successive order. The time periods of oscillations in the two cases are T1 and T2 respectively. If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is T. The correct relations is

View SolutionThe activation energies of two reactions are E1 & E2 with E1>E2. If temperature of reacting system is increased from T1 (rate constant are k1 and k2) to T2 (rate constant are k11 and k12) predict which of the following alternative is correct.
View Solution
