A mass m moving horizontal (along the x-axis) with velocity v collides and sticks to mass of 3m moving vertically upward (along the y-axis) with velocity 2v. The final velocity of the combination is
32vˆi+14vˆj
14vˆi+32vˆj
13vˆi+23vˆj
23vˆi+13vˆj
The correct Answer is:B
To find the final velocity of the combined mass after the collision, we can use the principle of conservation of momentum. Here are the steps to solve the problem:
Step 1: Identify the masses and their velocities
- Mass m1=m (moving horizontally with velocity v)
- Mass m2=3m (moving vertically with velocity 2v)
Step 2: Write down the momentum before the collision
The momentum before the collision can be expressed as the sum of the momenta of both masses:
- Momentum of m1 (horizontal):
→p1=m⋅v^i
- Momentum of m2 (vertical):
→p2=3m⋅2v^j=6mv^j
Step 3: Total momentum before the collision
The total momentum before the collision is:
→pinitial=→p1+→p2=mv^i+6mv^j
Step 4: Write down the total mass after the collision
After the collision, the two masses stick together, so the total mass mtotal is:
mtotal=m+3m=4m
Step 5: Let the final velocity be →vf
Let the final velocity of the combined mass be →vf. Then, the momentum after the collision is:
→pfinal=mtotal⋅→vf=4m⋅→vf
Step 6: Apply conservation of momentum
According to the conservation of momentum:
→pinitial=→pfinal
Substituting the expressions we derived:
mv^i+6mv^j=4m⋅→vf
Step 7: Simplify the equation
Dividing through by m:
v^i+6v^j=4→vf
Now, dividing both sides by 4 gives:
→vf=v4^i+6v4^j=v4^i+3v2^j
Final Result
The final velocity of the combination after the collision is:
→vf=v4^i+3v2^j
---
- Mass m1=m (moving horizontally with velocity v)
- Mass m2=3m (moving vertically with velocity 2v)
The momentum before the collision can be expressed as the sum of the momenta of both masses:
- Momentum of m1 (horizontal):
→p1=m⋅v^i
- Momentum of m2 (vertical):
→p2=3m⋅2v^j=6mv^j
The total momentum before the collision is:
→pinitial=→p1+→p2=mv^i+6mv^j
After the collision, the two masses stick together, so the total mass mtotal is:
mtotal=m+3m=4m
Let the final velocity of the combined mass be →vf. Then, the momentum after the collision is:
→pfinal=mtotal⋅→vf=4m⋅→vf
According to the conservation of momentum:
→pinitial=→pfinal
Substituting the expressions we derived:
mv^i+6mv^j=4m⋅→vf
Dividing through by m:
v^i+6v^j=4→vf
Now, dividing both sides by 4 gives:
→vf=v4^i+6v4^j=v4^i+3v2^j
The final velocity of the combination after the collision is:
→vf=v4^i+3v2^j
Similar Questions
A uniform rod of mass m and length / is hinged at upper end. Rod is free to rotate in vertical plane. A bail of mass m moving horizontally with velocity vo collides at lower end of rod perpendicular to it and sticks to it. The minimum velocity of the ball such that combined system just completes the vertical circle will be
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View Solution
Knowledge Check
A body of mass m, moving with velocity μ collides elasticity with another body at rest having mass M. If the body of mass M moves with velocity V, then the velocity of the body of mass m after the impact is
Am−Mm+MμBm−Mm+MVCm+MVm+MDmu−MVm
Particle A of mass mA=m2 moving along the x - axis with velocity v0 collides elastically with another particle B at rest having mass mB=m3 . If both particles move along the x - axis after the collision , the change Δλ in de - Broglie wavelength of particle A , in terms of its de - Broglie wavelength (λ0) before collision is :
View SolutionA particle of mass m moving with speed v in position x - direction collides perfectly inelastically with another identical particle moving with same speed in positive y - direction . Find final velocity of the combination.
View SolutionA ball of mass in m=1kg is hung vertically by a thread of length l=1.50m. Upper end of the thread is attached to the ceiling of a trolley of mass M=4kg. Initially, the trolley is stationary and it is free to move along horizontal rails without friction. A shell of mass m=1 kg, moving horizontally with velocity v0=6m/s collides with the ball and gets stuck with it. As a result, the thread starts to deflect towards right.
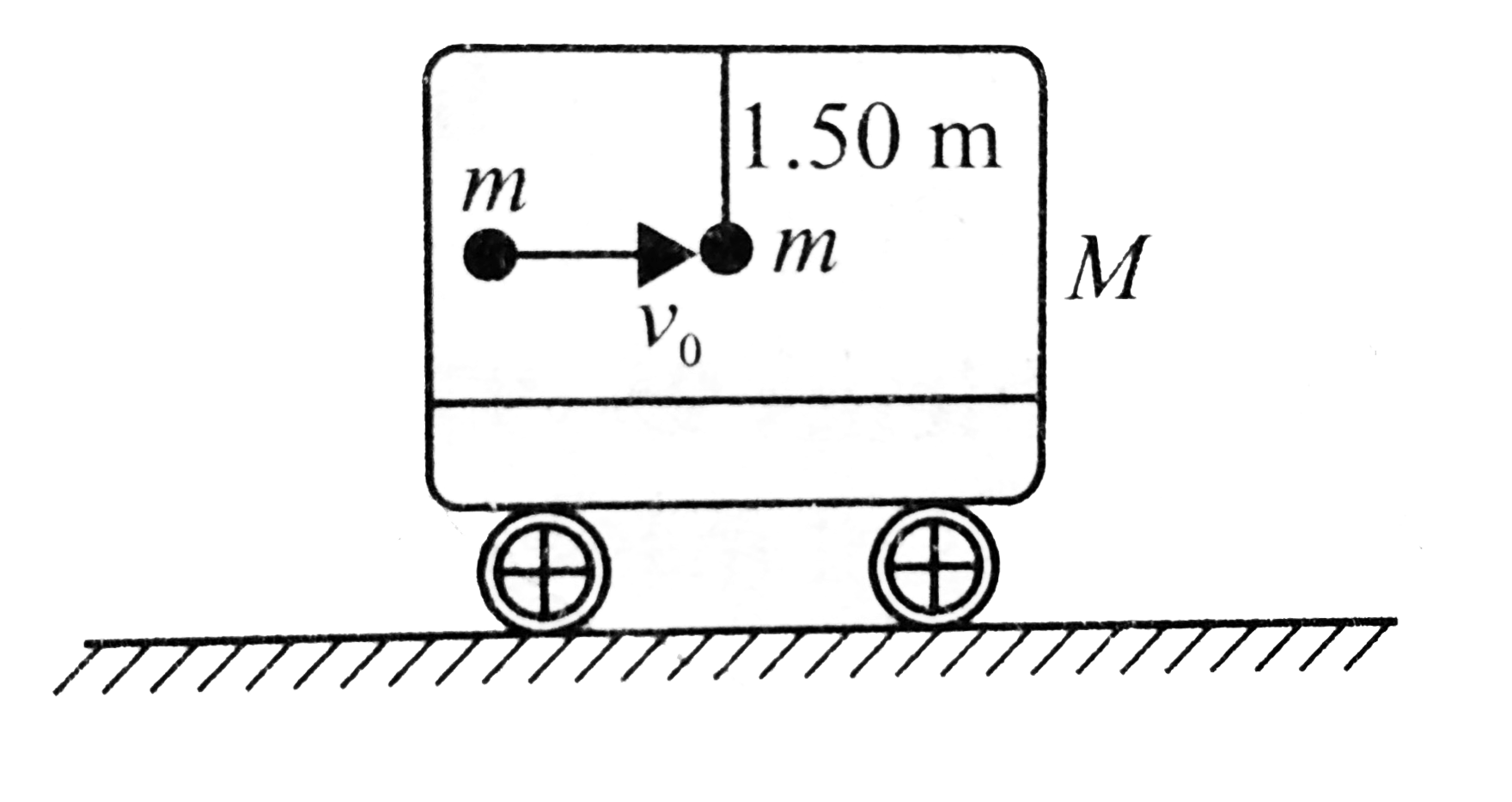
The velocity of the combined body just after collision is
View SolutionA body of mass m moving with a constant velocity v hits another body of the same mass moving with the same velocity v but in the opposite direction and sticks to it. The velocity of the compound body after collision is
View SolutionA body of mass m2 moving with velocity v0 collides elastically with another mass of m3 . Find % change in KE of first body
View SolutionA particle of mass m is moving along the x-axis with initial velocity ui . It collides elastically with a particle of mass 10 m at rest and then moves with half its initial kinetic energy (see figure).If sinθ1=√nsinθ2 then value of n is
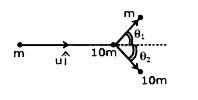
View SolutionA uniform cube of mass m and edge a moves on a horizontal surface along the positive x-axis, with initial velocity v0. Then
View Solution

