The total radiant energy per unit area, normal to the direction of incidence, received at a distance from the centre of a star of radius whose outer surface radiates as a black body at a temperature is given by
(where is Stefan's constant)
The correct Answer is:A
To solve the problem of finding the total radiant energy per unit area received at a distance R from the center of a star, we can follow these steps:
1. Understand the Concept of Black Body Radiation:
A star behaves like a black body radiator. According to Stefan-Boltzmann law, the total energy radiated per unit area of a black body is given by:
E=σT4
where σ is Stefan's constant and T is the temperature of the black body.
2. Calculate the Total Energy Radiated by the Star:
The total energy radiated by the star can be calculated by multiplying the energy per unit area by the surface area of the star. The surface area A of a sphere (the star) is given by:
A=4πr2
Thus, the total energy Etotal radiated by the star is:
Etotal=σT4⋅4πr2
3. Determine the Intensity at Distance R:
The intensity I (which is energy per unit area) at a distance R from the star is given by the total energy radiated divided by the area over which this energy is spread. The area of a sphere with radius R is:
AR=4πR2
Therefore, the intensity I can be expressed as:
I=EtotalAR=σT4⋅4πr24πR2
4. Simplify the Expression:
The 4π terms cancel out:
I=σT4r2R2
5. Final Result:
The total radiant energy per unit area received at a distance R from the star is:
I=σr2T4R2
A star behaves like a black body radiator. According to Stefan-Boltzmann law, the total energy radiated per unit area of a black body is given by:
E=σT4
where σ is Stefan's constant and T is the temperature of the black body.
The total energy radiated by the star can be calculated by multiplying the energy per unit area by the surface area of the star. The surface area A of a sphere (the star) is given by:
A=4πr2
Thus, the total energy Etotal radiated by the star is:
Etotal=σT4⋅4πr2
The intensity I (which is energy per unit area) at a distance R from the star is given by the total energy radiated divided by the area over which this energy is spread. The area of a sphere with radius R is:
AR=4πR2
Therefore, the intensity I can be expressed as:
I=EtotalAR=σT4⋅4πr24πR2
The 4π terms cancel out:
I=σT4r2R2
The total radiant energy per unit area received at a distance R from the star is:
I=σr2T4R2
Similar Questions
The sun having surface temperature Ts radiates like a black body. The rasius of sun is Rs and earth is at a distance R from the surface of sun. Earth absorbs radiations falling on its surface from sun only and is at constant temperature T. If radiations falling on earth's surface are alomost parallel and earth also radiates like a blackbody, then
View SolutionAssuming the sun to have a spherical outer surface of radius r radiating like a black body at temperature t∘C. The power received by a unit surface (normal to the incident rays) at a distance R from the centre of the sun is
where σ is the Stefan's constant.
View SolutionThe radiations emitted by the sun are analyzeed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
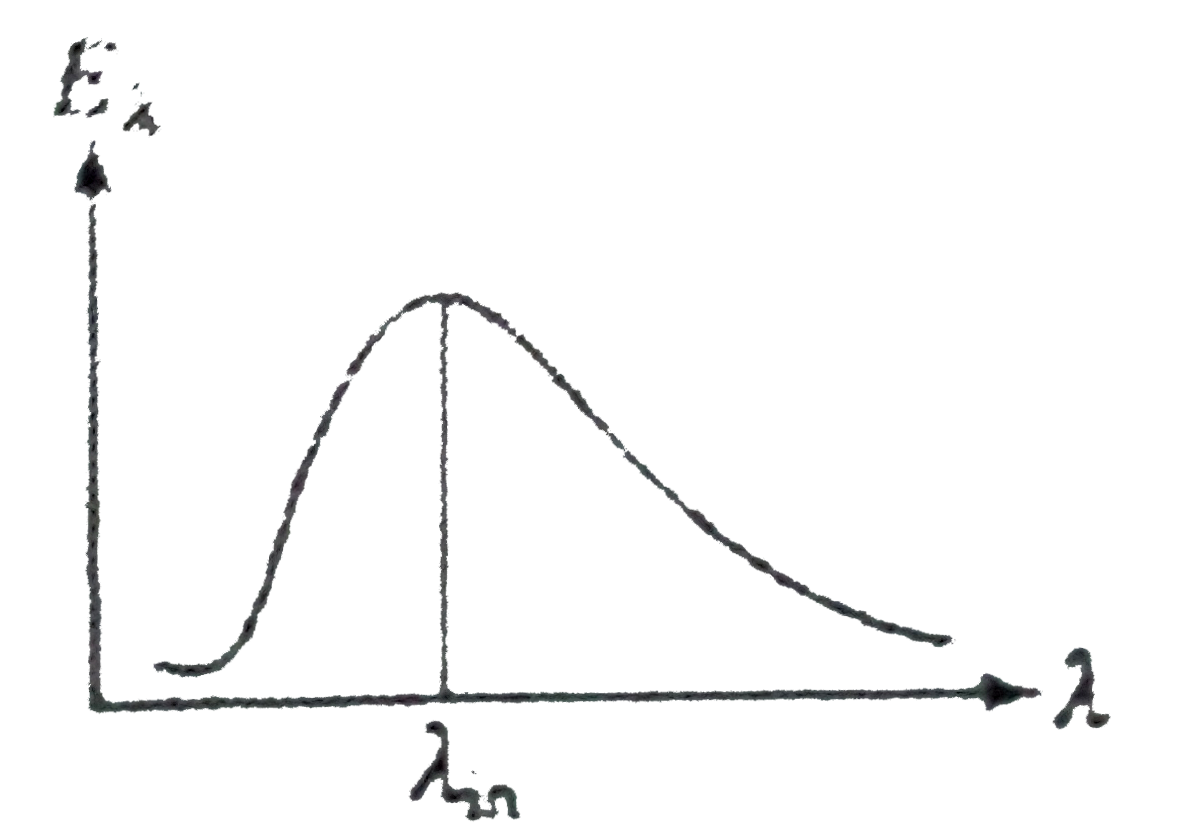
If the earth is at a distance 'd' from the sun the intensity of light falling on the earth (called solar constant S) is
View SolutionLet us assume that sun radiates like a black body with surface temperature at T0=6000K and earth absorbs radiation coming from sun only. If both earth and sun are considered perfect spheres with distance between centre of earth and centre of sun to be 200 times the radius of sun, find the temperature (in Kelvin) of surface of earth in steady state (assume radiation incident on earth to be almost parallel).
View SolutionThe radiations emitted by the sun are analyzed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
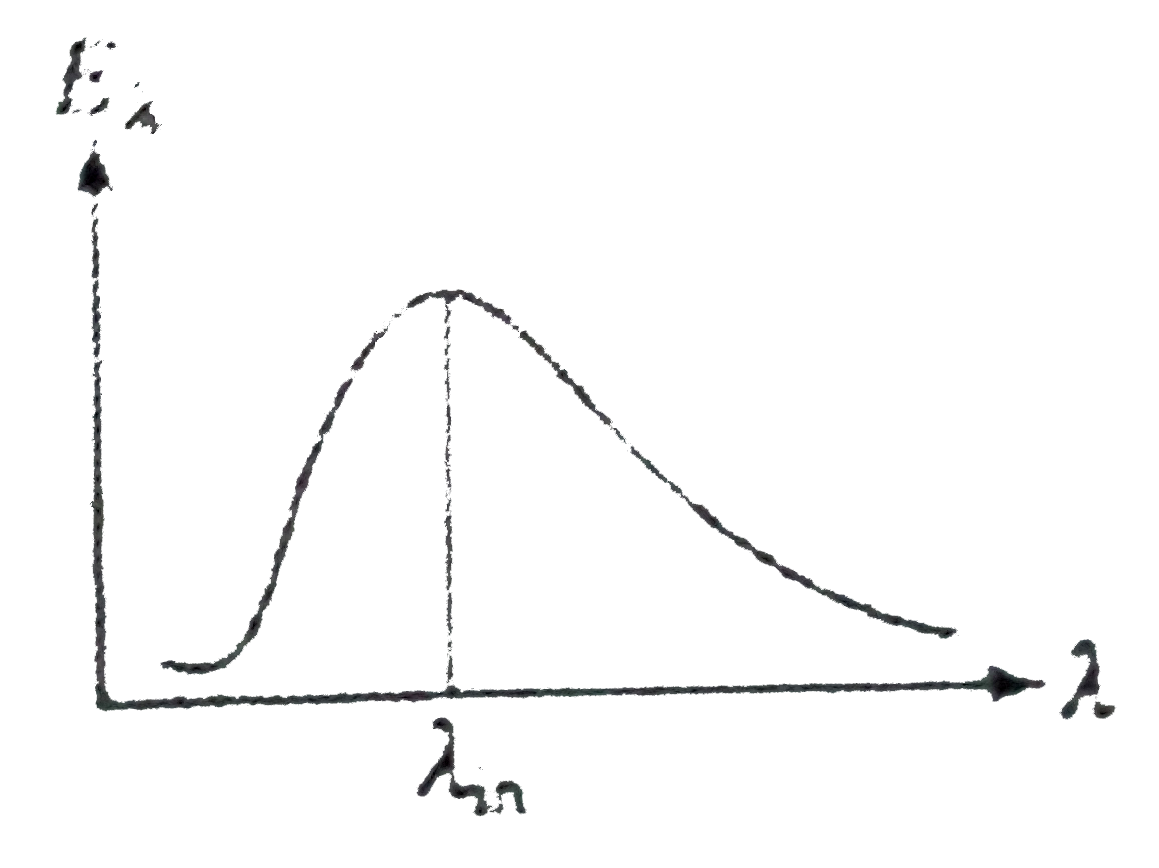
Assume the sun produces energy only by nuclear fusion of hydrogen nuclei and the fraction of nuclear mass of hydrogen that can be converted to energy is η. How long will the sun keep on emittied the energy if the mass of hydrogen at present in Sun's core is m?
View SolutionAssuming the sun to be a spherical body (e = 1) of radius R at a temperature of T K, evaluate the total radiant power, incident on Earth having radius r0, at a distance r from the sun, where r0 is the radius of the earth and σ is Stefan's constant.
View SolutionThe surface temperature of the sun is T0 and it is at average distance d from a planet. The radius of the sun is R. The temperature at which planet radiates the energy is
View SolutionOne end of a rod of length 20cm is inserted in a furnace at 800K The sides of the rod are covered with an insulating material and the other end emits radiation like a black body. The temperature of this end is 750K in the steady state The temperature of the surrounding air is 300K Assuming radiation to be the only important mode of energy transfer between the surrounding and the open end of the rod, find the thermal conductivity of the rod Stefan's constant σ=6.0×10−8Wm−2K−4 .
View SolutionThe potential energy function of a particle is given by U(r)=A2r2−B3r, where A and B are constant and r is the radial distance from the centre of the force. Choose the correct option (s)
View SolutionThe solar constant is the amount of heat energy received per second per unit area of a perfectly black surface placed at a mean distance of the Earth form the Sun, in the absence of Earth's atmosphere, the surface being held perpendicular to the direction of Sun's rays. Its value is 1388W/m2. If the solar constant for the earth is 's'. The surface temperature of the sun is TK,D is the diameter of the sun, R is the mean distance of the Earth from the sun. The sun subtends a small angle 'theta' at the earth. Then correct options is/are:-
View Solution