The sun having surface temperature Ts radiates like a black body. The rasius of sun is Rs and earth is at a distance R from the surface of sun. Earth absorbs radiations falling on its surface from sun only and is at constant temperature T. If radiations falling on earth's surface are alomost parallel and earth also radiates like a blackbody, then
T=Ts√Rs2R
T=Ts
T=Ts2√(RsR)
T=Ts√(RsR)
The correct Answer is:A
To solve the problem, we will use the principles of black body radiation and the Stefan-Boltzmann law. Here’s a step-by-step solution:
Step 1: Understand the situation
The sun radiates energy as a black body, and the Earth, which is at a distance R from the surface of the sun, absorbs this radiation. The Earth is also treated as a black body and is at a constant temperature T.
Step 2: Use the Stefan-Boltzmann Law
The power emitted by a black body is given by the Stefan-Boltzmann law:
P=σAT4
where σ is the Stefan-Boltzmann constant, A is the surface area, and T is the temperature.
Step 3: Calculate the power emitted by the Sun
The surface area of the Sun As is:
As=4πR2s
Thus, the power emitted by the Sun Ps is:
Ps=σAsT4s=σ(4πR2s)T4s
Step 4: Calculate the intensity of radiation at the Earth
The intensity I of the radiation at a distance R from the Sun is given by the power per unit area:
I=Ps4πR2=σ(4πR2s)T4s4πR2=σR2sT4sR2
Step 5: Calculate the power absorbed by the Earth
The Earth has a radius r, and its projected area Ae is:
Ae=πr2
The power Pe absorbed by the Earth is:
Pe=I⋅Ae=(σR2sT4sR2)⋅πr2
Step 6: Set the power absorbed equal to the power emitted
At thermal equilibrium, the power absorbed by the Earth equals the power emitted by the Earth:
Pe=σAeT4
Substituting for Pe:
(σR2sT4sR2)⋅πr2=σ(πr2)T4
Step 7: Simplify the equation
We can cancel σ and πr2 from both sides:
R2sT4sR2=T4
Step 8: Solve for T
Rearranging gives:
T4=R2sT4sR2
Taking the fourth root:
T=(R2sR2)1/4Ts=R1/2sR1/2Ts
Final Expression
Thus, the temperature of the Earth is given by:
T=Ts(RsR)1/2
The sun radiates energy as a black body, and the Earth, which is at a distance R from the surface of the sun, absorbs this radiation. The Earth is also treated as a black body and is at a constant temperature T.
The power emitted by a black body is given by the Stefan-Boltzmann law:
P=σAT4
where σ is the Stefan-Boltzmann constant, A is the surface area, and T is the temperature.
The surface area of the Sun As is:
As=4πR2s
Thus, the power emitted by the Sun Ps is:
Ps=σAsT4s=σ(4πR2s)T4s
The intensity I of the radiation at a distance R from the Sun is given by the power per unit area:
I=Ps4πR2=σ(4πR2s)T4s4πR2=σR2sT4sR2
The Earth has a radius r, and its projected area Ae is:
Ae=πr2
The power Pe absorbed by the Earth is:
Pe=I⋅Ae=(σR2sT4sR2)⋅πr2
At thermal equilibrium, the power absorbed by the Earth equals the power emitted by the Earth:
Pe=σAeT4
Substituting for Pe:
(σR2sT4sR2)⋅πr2=σ(πr2)T4
We can cancel σ and πr2 from both sides:
R2sT4sR2=T4
Rearranging gives:
T4=R2sT4sR2
Taking the fourth root:
T=(R2sR2)1/4Ts=R1/2sR1/2Ts
Thus, the temperature of the Earth is given by:
T=Ts(RsR)1/2
Similar Questions
The surface temperature of the sun is T0 and it is at average distance d from a planet. The radius of the sun is R. The temperature at which planet radiates the energy is
View SolutionIn the absence of greenhouse gases, the temperature of earth's surface will fall to
View SolutionIn the absence of greenhouse gases, the temperature of earth's surface will fall to
View SolutionIf the temperature of the sun (black body) is doubled, the rate of energy received on earth will be increase by a factor of
View SolutionIf the earth be one-half of its present distance from the sun, how many days will be in one year ?
View SolutionThe largest and the shortest distance of the earth from the sun are r1 and r2, its distance from the sun when it is at the perpendicular to the major axis of the orbit drawn from the sun
View SolutionA body which is initially at rest at a height R above the surface of the earth of radius R, falls freely towards the earth. Find out its velocity on reaching the surface of earth. Take g= acceleration due to gravity on the surface of the Earth.
View SolutionA body at rest starts from a point at a distance r (gtR) from the centre of the Earth. If M and R stand for the speed of the body when it reaches the Earth surface is
View SolutionAt what height from the surface of the earth, the total energy of satellite is equal to its potential energy at a height 2R from the surface of the earth (R=radius of earth)
View SolutionThe radiations emitted by the sun are analyzeed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
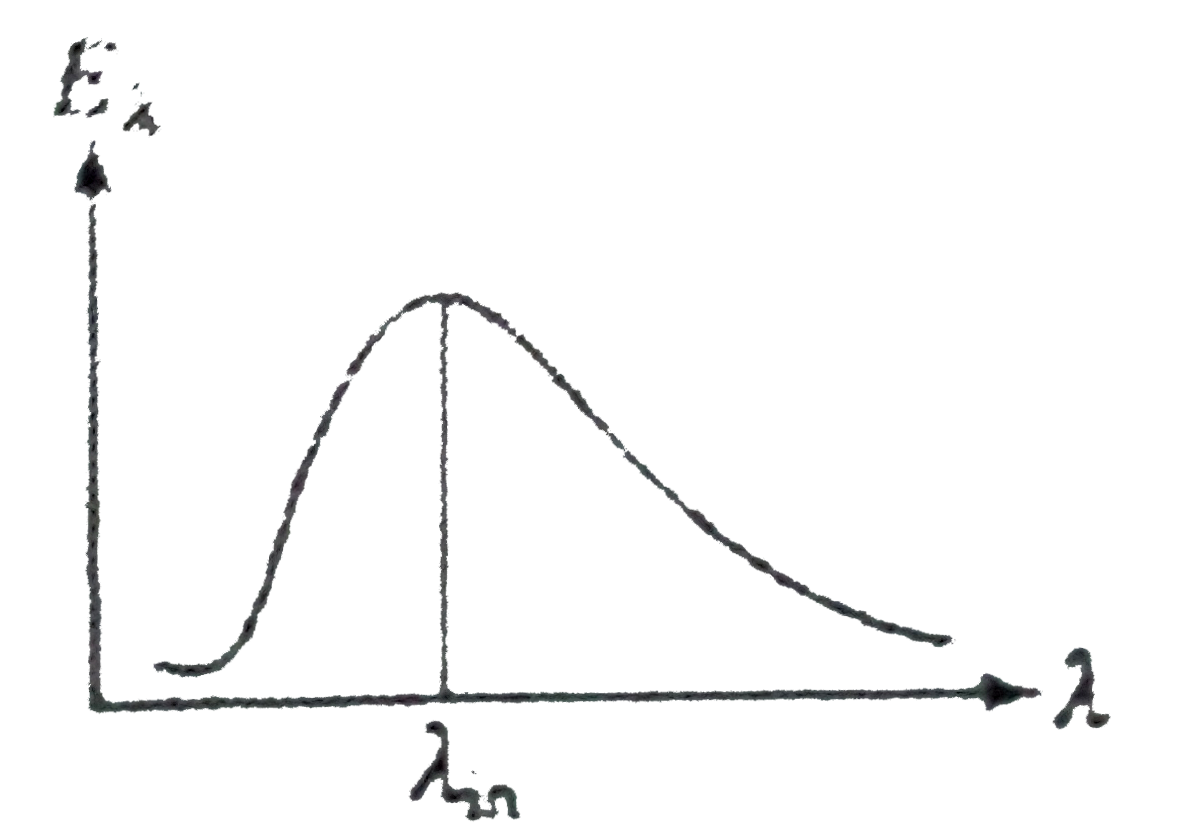
If the earth is at a distance 'd' from the sun the intensity of light falling on the earth (called solar constant S) is
View Solution
