The unit of thermal conductivity is :
Wm−1K−1
Jm−1K−1
Jm−1K−1
WmK−1
The correct Answer is:A
To find the unit of thermal conductivity, we start with the formula for thermal conductivity (K):
K=Q⋅DA⋅ΔT
Where:
- Q is the amount of heat transferred (measured in Joules or Watts),
- D is the distance between the two isothermal planes (measured in meters),
- A is the area of the surface (measured in square meters),
- ΔT is the temperature difference (measured in Kelvin).
Step 1: Identify the units of each variable
- The unit of heat transferred Q is Watts (W).
- The unit of distance D is meters (m).
- The unit of area A is square meters (m²).
- The unit of temperature difference ΔT is Kelvin (K).
Step 2: Substitute the units into the formula
Now we substitute these units into the formula for thermal conductivity:
K=Q⋅DA⋅ΔT
Substituting the units:
K=W⋅mm2⋅K
Step 3: Simplify the expression
Now we simplify the expression:
K=W⋅mm2⋅K=Wm⋅K
Final Result
Thus, the unit of thermal conductivity K is:
K=Wm⋅K
This can also be written as:
K=W/m⋅K
Conclusion
The unit of thermal conductivity is Watt per meter Kelvin (W/m·K).
---
- Q is the amount of heat transferred (measured in Joules or Watts),
- D is the distance between the two isothermal planes (measured in meters),
- A is the area of the surface (measured in square meters),
- ΔT is the temperature difference (measured in Kelvin).
- The unit of heat transferred Q is Watts (W).
- The unit of distance D is meters (m).
- The unit of area A is square meters (m²).
- The unit of temperature difference ΔT is Kelvin (K).
Now we substitute these units into the formula for thermal conductivity:
Now we simplify the expression:
Thus, the unit of thermal conductivity K is:
The unit of thermal conductivity is Watt per meter Kelvin (W/m·K).
Similar Questions
Knowledge Check
Two rods of length l1andl2 and coefficients of thermal conductivities k1andK2 are kept touching each other. Both have the same area of cross-section. The equivalent of thermal conductivity is
AK1+K2BK1l1+K2l2CK1l1+K2l2l1+l2Dl1+l2(l1/K1)+(l2/K2)
The dimensions of coefficient of thermal conductivity is
View SolutionCoefficient of thermal conductivity has the dimensions:
View SolutionThree rods of same dimension are joined in series having thermal conductivity k1 , k2 and k3. The equivalent thermal conductivity is
View Solution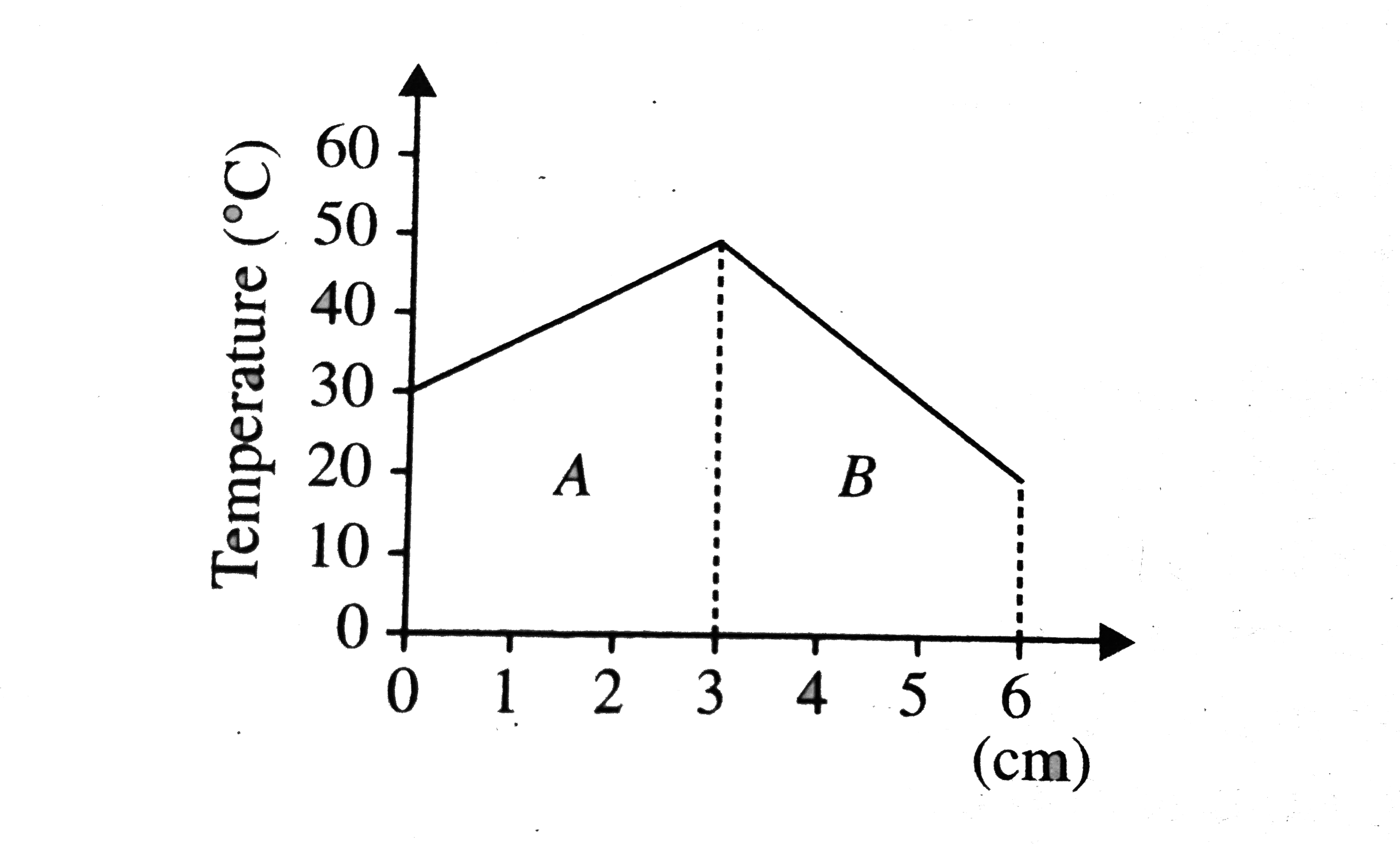
The temperature across two different slabs A and B are shown I the steady state (as shown Fig) The ratio of thermal conductivities of A and B is
View Solution
The temperature across two different slabs A and B are shown I the steady state (as shown Fig) The ratio of thermal conductivities of A and B is
View SolutionThe ratio of thermal conductivity of two rods of different material is 5:4. The two rods of same area of cross-section and same thermal resistance will have the lengths in the ratio
View SolutionCoefficient of thermal conductivity is the product of heat, distance and reciprocal of (area x difference in temperature x time). The new value of a unit of coefficient of thermal conductivity, if fundamental units are 21.6 kg, 1 decimetre, 4 K and 1 minute will be ______ ×10−6 new units.
View Solution