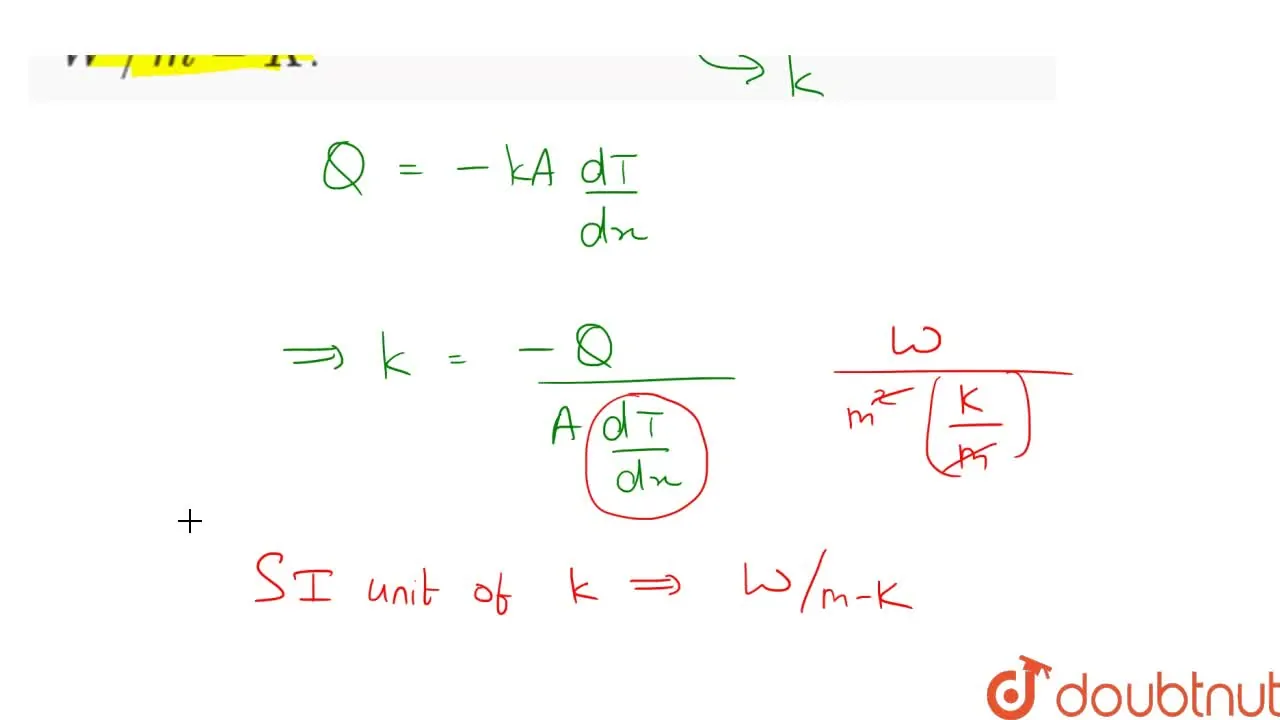Show that the SI units of thermal conductivity are W/m−K.
The correct Answer is:A
Q=(KA(θ1−θ2)tl)
∴K=QlA(θ1−θ2)t=J−mm2K−s
=Wm−K(asJ/s=W) .
Related Playlists
- BOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Assertion And Reason10videos
CALORIMETRY & HEAT TRANSFER
- BOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 1 Objective11videos
CALORIMETRY & HEAT TRANSFER
- BOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Exercise 22.17videos
CALORIMETRY & HEAT TRANSFER
- BOOK - DC PANDEY ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise13videos
BASIC MATHEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery38videos
CALORIMETRY AND HEAT TRANSFER
Similar Questions
The unit of thermal conductivity is :
View SolutionThe unit of thermal conductivity is :
View SolutionSI unit of energy
View SolutionSI unit of voltage
View SolutionA composite slab is made of two parallel layers of two different materials of thermal conductivities K1andK2 are of same thickness. Show that the equivalent thermal conductivity of the slab is 2K1K2K1+K2
View SolutionSI unit of coefficient of thermal conductivity
View SolutionFind SI units of thermal resistance.
View SolutionA cylinder of radius r made of a material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius r and outer radius 2r made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. Show that the effective thermal conductivity of the system is (K1+3K2)/4.
View SolutionThe plane wall of an oven is of thickness L = 0.05 m and is exposed to the surrounding at 300 K. The outer surface of the oven exposed to the surrounding is at temperature 320 K in steady state. The energy radiated (In W/m2) by outer surface is proportional to the temperature difference between the surface and the surrounding, with proportionality constant 20W/m2K. What is the temperature of inner surface of the oven in steady state if the wall has a thermal conductivity of K = 0.5 W/mK
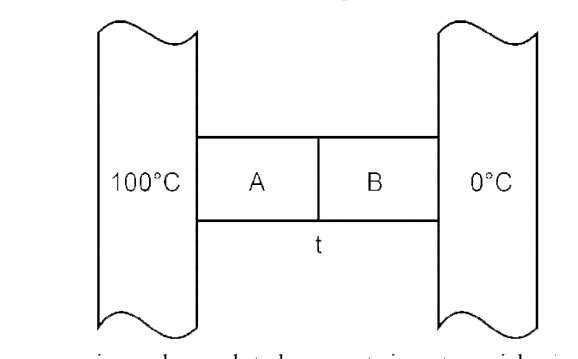
View SolutionTwo metal cubes A and B of same size are arranged as shown in Figure. The extreme ends of the combination are maintained at the indicated temperatures. The arrangement is thermally insulated. The coefficients of thermal conductivity of A and B are 300W/m∘Cand200W/m∘C, respectively. After steady state is reached the temperature t of the interface will be ......
 View Solution
View Solution