What should be the ratio of area of cross section of the master cylinder and wheel cylinder of a hydraulic brake so that a force of 15 N can be obtained at each of its brake shoe by exerting a force of 0.5 N on the pedal ?
To solve the problem, we need to find the ratio of the area of cross-section of the master cylinder (A1) to the area of cross-section of the wheel cylinder (A2) in a hydraulic brake system. We are given the forces applied and the forces obtained at the brake shoes.
1. Identify the Given Values:
- Force exerted on the pedal (F1) = 0.5 N
- Force obtained at each brake shoe (F2) = 15 N
2. Understand the Principle of Hydraulic Brakes:
- In a hydraulic brake system, the pressure applied in the master cylinder is transmitted to the wheel cylinder. According to Pascal's law, the pressure is the same in both cylinders.
- The pressure (P) is defined as force (F) per unit area (A):
P=FA
3. Set Up the Pressure Equality:
- The pressure in the master cylinder (P1) is equal to the pressure in the wheel cylinder (P2):
P1=P2
- This can be expressed as:
F1A1=F2A2
4. Rearranging the Equation:
- From the equation above, we can rearrange it to find the ratio of the areas:
A1A2=F1F2
5. Substituting the Values:
- Substitute the known values into the equation:
A1A2=0.515
6. Simplifying the Ratio:
- Simplify the fraction:
0.515=130
- Therefore, we have:
A1A2=130
7. Final Ratio:
- The required ratio of the area of cross-section of the master cylinder to the area of cross-section of the wheel cylinder is:
A1:A2=1:30
Conclusion:
The ratio of the area of cross-section of the master cylinder to the wheel cylinder is 1:30.
- Force exerted on the pedal (F1) = 0.5 N
- Force obtained at each brake shoe (F2) = 15 N
- In a hydraulic brake system, the pressure applied in the master cylinder is transmitted to the wheel cylinder. According to Pascal's law, the pressure is the same in both cylinders.
- The pressure (P) is defined as force (F) per unit area (A):
P=FA
- The pressure in the master cylinder (P1) is equal to the pressure in the wheel cylinder (P2):
P1=P2
- This can be expressed as:
F1A1=F2A2
- From the equation above, we can rearrange it to find the ratio of the areas:
A1A2=F1F2
- Substitute the known values into the equation:
A1A2=0.515
- Simplify the fraction:
0.515=130
- Therefore, we have:
A1A2=130
- The required ratio of the area of cross-section of the master cylinder to the area of cross-section of the wheel cylinder is:
A1:A2=1:30
The ratio of the area of cross-section of the master cylinder to the wheel cylinder is 1:30.
Topper's Solved these Questions
- FLUIDSBOOK - ICSECHAPTER - FLUIDSEXERCISE - TOPIC 1 (3 Marks Questions )
18 Videos
- FLUIDSBOOK - ICSECHAPTER - FLUIDSEXERCISE - TOPIC 1 (4 Marks Questions )
10 Videos
- ELECTRICITY AND MAGNETISM BOOK - ICSECHAPTER - ELECTRICITY AND MAGNETISM EXERCISE - TOPIC 2 Magnetism (4 Marks Questions )
6 Videos
- HEAT AND ENERGYBOOK - ICSECHAPTER - HEAT AND ENERGYEXERCISE - EXERCISE -6(D) Multiple Choice Question)
4 Videos
Similar Questions
What is the area of cross-section of a body in m2, when it exerts a force of 50 N and produces a pressure of 2000 Pa?
View SolutionIn a hydraulic machine, the two pistons are of area of cross section in the ratio 1:10. What weight force in needed on the narrow piston to overcome a force of 100 N on the wide piston?
View SolutionThe area of cross sectioin of the two arms of a hydraulic press is 1cm2 and 20cm2 respectively. A force of 10N is applied on the water in the thinner arm. What force should be applid on the water in the thicker arms so that water may remain in equilibrium?

View SolutionA cross-section of a solid cylinder is shown in Fig. 7.2.20, with the core section protruding from the larger drum. A rope wrapped around the drum of radius r1=80 cm exerts a force 10.0 N to the right on the cylinder. The cylinder can rotate freely around the central axis. A rope wrapped around the core of radius r2=40cm exerts a force of 15.0 N downwards on the cylinder, (a) Calculate the net torque acting on the cylinder about the axis of rotation ?

View SolutionThe area of cross section of the two arms of a hydraulilc press are 1 cm^2 and 10 cm^2 respectively figure. A force of 5N is applied on the water in the thinner arm. What force should be applied on the water in the thicker arm so that the water may remain in equilibrium?
 ,
,
View SolutionThe area of cross section of the two arms of a hydraulilc press are 1 cm^2 and 10 cm^2 respectively figure. A force of 5N is applied on the water in the thinner arm. What force should be applied on the water in the thicker arm so that the water may remain in equilibrium?
 ,
,
View SolutionWhat force is applied on a piston of area of cross section 2cm2 to obtain a force 150 N on the piston of area of cross section 12cm2 in a hydraulic machine ?
View SolutionA liquid of density ρ is flowing with a speed v through a pipe of cross sectional area A. The pipe is bent in the shape of a right angles as shown. What force should be exerted on the pipe at the corner to keep it fixed?
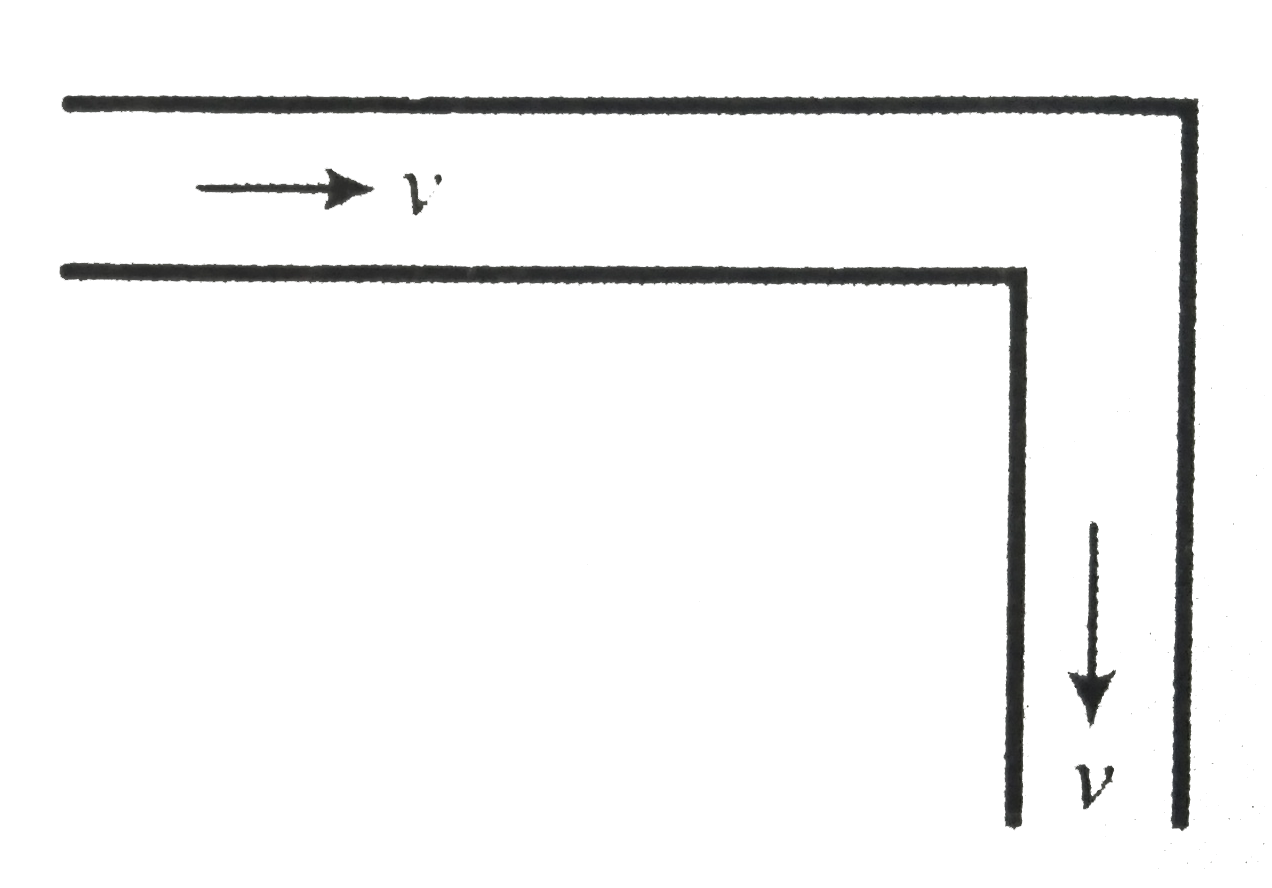
View SolutionA force of 10 N acts on a body of mass 0.5 kg for 0.25s starting from rest.What is its momentum now?
View SolutionThe area of cross-section of the two vertical arms of a hydraulic press are 1 cm2 and 10cm2 respectively. A force of 10N applied. As shown in the figure, to a tight fitting light piston in the thinner arm balances a force F applied to the corresponding piston in the thicker arm. Assuming that the levels of water in both the arms are the same, we can conclude:-

View Solution
