Median = __________ quartileSolution in Bengali
First
Second
Third
none of these
Step by step video & image solution for Median = __________ quartile by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Standand deviation of the 6 numbers 5, 5, 5, 7, 7, 7 is
View SolutionDivision obtained in an examination is
View SolutionFind the lower quartile,upper quartile and inter quartile range for the date 19,17,13,7
View SolutionFind inter quartile range, quartile deviation and coefficient of quartile deviation from the following data:
View SolutionCalculate inter quartile range, quartile deviation and the coefficient of quartile deviation from the following data:
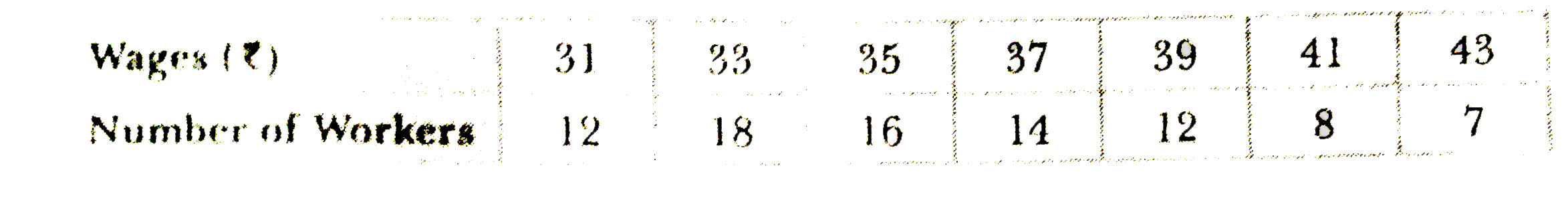
View SolutionDifference between third quartile and first quartile of a series, is called ……………..
(Quartile Deviation/Inter Quartile Range)
View SolutionEstimate quartile deviation and the coefficient of quartile deviation of the following data: 8,9,11,12,13,17,20,21,23,25,27 Show that QD is the average of the difference between two quartiles.
View SolutionQuartiles
View SolutionSpot the wrong statement about median and quartiles.
View SolutionIf the quartile deviation of a set of observations is 10 and the third quartile is 35, then the first quartile is
View SolutionIf the mean of the lower quartile and upper quartile is 10 and the semi-interquartile range is 5 , then the lower quartile and the upper quartile are ______ and _______ .
View SolutionThe statistics below provide a summary of IQ scores of 100 children.
Mean:100
Median:102
Standard Deviation:10
First Quartile:84
Third Quartile:110
About 50 of the children in this sample have IQ scores that are
View SolutionIf the quartile deviation is 1.79 and the first quartile is 5.86. Find the third quartile.
View SolutionFind the median and upper quartile for the following data : 9,5,7,11,13,17,15.
View SolutionIf the 1st and 3rd quartiles of a symmetrical distribution are 11 and 17 respectively, then what is the value of the median of that distribution?
View Solution

