यदि a,b,c,d,e,f समांतर श्रेढ़ी में हैं। तब e−c बराबर है -
2(c−a)
d−b
2(f−d)
d−c
The correct Answer is:B
a, b, c, d, e, f समांतर श्रेढ़ी में हैं।
मान लीजिए सार्व अंतर = D
∴e−c=(a+4D)–(a+2D)=2D
=2(d−c)
Topper's Solved these Questions
- JEE- MAIN TEST 1Book:NTA MOCK TESTSChapter:JEE- MAIN TEST 1Exercise:गणित (विषयपरक आंकिक)
Explore 5 Videos
- JEE MAIN TEST-98Book:NTA MOCK TESTSChapter:JEE MAIN TEST-98Exercise:गणित (विषयपरक आंकिक)
Explore 5 Videos
- JEE- MAIN TEST 2Book:NTA MOCK TESTSChapter:JEE- MAIN TEST 2Exercise:गणित (विषयपरक आंकिक)
Explore 5 Videos
Similar Questions
यदि f (x) एक बहुपद है जो f(x)f(1x)=f(x)+f(1x) और F(2)>1 को संतुष्ट करता है, तब limx→1f(x) है
View Solutionमाना f (x) एक संतत और धनात्मक फलन इस प्रकार कि y=f(x), x-अक्ष और रेखाओं x2=2ax द्वारा परिबद्ध क्षेत्रफल 6a2+sina(∀a>0) वर्ग इकाई है। यदि f(π)=kπ , तब k का मान बराबर है:
View Solution26,28,30 इकाई भुजा वाले त्रिभुज की अंतः त्रिज्या है
View SolutionIf in two triangles ABC and DEF , ABDE=BCFE=CAFD , then FDECAB (b) FDEABC (c) CBAFDE (d) BCAFDE
View SolutionD, E, F are the mid-point of the sides BC, CA and AB respectively of ABC. Then DEF is congruent to triangle. ABC (b) AEF (c) BFD, CDE (d) AFE, BFD, CDE
Given : D, E, F are the mid-point of the sides BC, CA and AB .
View SolutionIn Figure, AB⊥BEandFE⊥BE.If BC=DEandAB=EF, then ABD is congruent to:
(a)EFC
(b) ECF
(c) CEF
(d) FEC
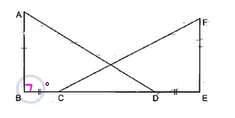
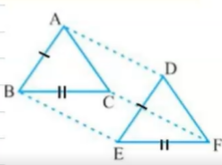
View SolutionIf ABC and DEF are two triangles such that AB, BC are respectively equal and parallel to DE, EF, then show that Quadrilateral ABED is a parallelogram Quadrilateral BCFE is a parallelogram AC=DF (iv) ABC ≅ DEF
View Solutiona d c e b e d f e h e ?
View Solutionयदि →a=→b+→c, तब →a.(→b×→c) बराबर है -
View Solutionमाना धनात्मक संख्याएँ a,b,c,d समान्तर श्रेढ़ी में हैं। तब abc,abd,acd,bcd = ?
View Solutionयदि ∫x5e−x2dx=g(x)e−x2+c है, जहाँ c एक समाकलन अचर है तो g(−1) बराबर है
View Solutionयदि 3x=4x−1 तब x बराबर है
View Solutionयदि A = {a,b}, B = {c,d}, C= {d,e} , तब {(a,c),(a,d),(a,e),(b,c),(b,d),(b,e)} =
View SolutionIn Figure, DE∣∣AC and DF∣∣AE . Prove that EFBF=ECBE .
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=34 , then write Area (ABC):Area(DEF) .
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=25 , then Area(ABC):Area(DEF)=
View Solution