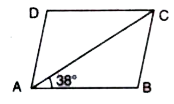
ABCD is a rhombus. If ∠BCA=35∘,and∠ADC.
The correct Answer is:110∘.
To solve the problem step by step, we will follow the reasoning provided in the video transcript.
Step 1: Understand the Properties of the Rhombus
A rhombus is a type of quadrilateral where all sides are equal, and the diagonals bisect each other at right angles (90 degrees). This means that the diagonals divide the rhombus into four right triangles.
Hint: Recall the properties of a rhombus, particularly how its diagonals interact with the angles.
Step 2: Set Up the Problem
We are given that angle BCA = 35 degrees. We need to find angle ADC. Let's denote angle ADC as X.
Hint: Label the angles clearly in your diagram to avoid confusion.
Step 3: Identify Relevant Angles
In triangle OBC (where O is the intersection of the diagonals), we know:
- Angle BCA = 35 degrees
- Angle OBC = X/2 (because angles on either side of the diagonal are equal)
Hint: Use the property of angles being equal when split by a diagonal.
Step 4: Apply the Angle Sum Property of Triangle OBC
The sum of the angles in triangle OBC is equal to 180 degrees. Therefore, we can write the equation:
Angle OBC+Angle BOC+Angle BCA=180∘
Substituting the known values:
X2+90∘+35∘=180∘
Hint: Remember that one angle in triangle OBC is 90 degrees due to the properties of the rhombus.
Step 5: Simplify the Equation
Now, simplify the equation:
X2+125∘=180∘
Subtract 125 degrees from both sides:
X2=180∘−125∘
X2=55∘
Hint: Keep track of your arithmetic to ensure accuracy.
Step 6: Solve for X
Now, multiply both sides by 2 to find X:
X=2×55∘
X=110∘
Hint: Double-check your multiplication to confirm the final value.
Conclusion
Thus, angle ADC = 110 degrees.
Final Answer: Angle ADC = 110 degrees.
A rhombus is a type of quadrilateral where all sides are equal, and the diagonals bisect each other at right angles (90 degrees). This means that the diagonals divide the rhombus into four right triangles.
We are given that angle BCA = 35 degrees. We need to find angle ADC. Let's denote angle ADC as X.
In triangle OBC (where O is the intersection of the diagonals), we know:
- Angle BCA = 35 degrees
- Angle OBC = X/2 (because angles on either side of the diagonal are equal)
The sum of the angles in triangle OBC is equal to 180 degrees. Therefore, we can write the equation:
Angle OBC+Angle BOC+Angle BCA=180∘
Substituting the known values:
X2+90∘+35∘=180∘
Now, simplify the equation:
X2+125∘=180∘
Subtract 125 degrees from both sides:
X2=180∘−125∘
X2=55∘
Now, multiply both sides by 2 to find X:
X=2×55∘
X=110∘
Thus, angle ADC = 110 degrees.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A rhombus has :
Aone line of symmetryBtwo lines of symmetry eachCfour lines of symmetryDno line of symmetry
In a rhombus ABCD if ∠ACB=40∘, then fine ∠ADC.
View SolutionIn a rectangle ABCD, diagonals AC and BD intersect at O. If ∠OAB=35∘, find :
(a)∠ABC(b)∠ABO(c)∠COD(d)∠BOC)
View SolutionIn the given figure, ABCD is a rhombus with angle A=67∘
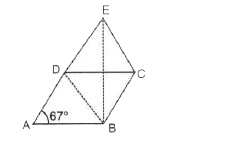
If DEC is an equilateral triangle, calculate:
∠CBE
View SolutionIn the given figure, ABCD is a rhombus with angle A=67∘
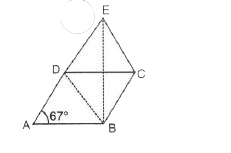
If DEC is an equilateral triangle, calculate:
∠DBE
View SolutionDiagonals of a quadrilateral ABCD bisect each other. If ∠A=35∘, determine ∠B.
View SolutionIn the given figure, ABCD is a rhombus with angle A = 67∘.
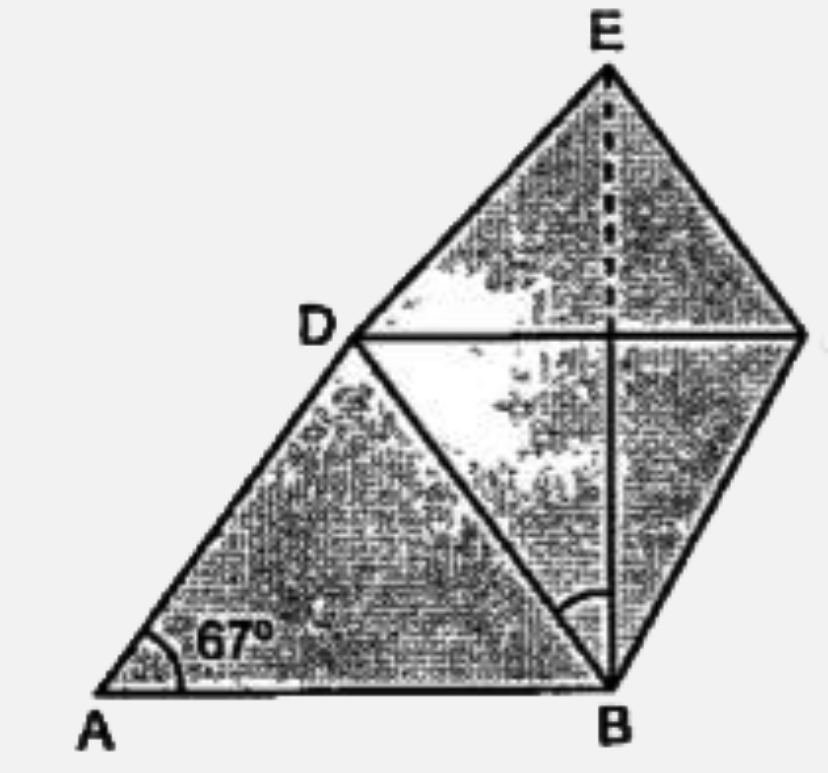
If DEC is an equilateral triangle. Calculate :
(i) ∠CBE (ii) ∠DBE
View SolutionIn the adjoining figure, ABCD is a rhombus and ABE is an equilateral triangle. If ∠BCD=70∘, find
(a)∠ADE (b)∠BDE (c)∠BED

View Solution