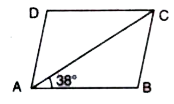
ABCD is a rhombus such that , then is
The correct Answer is:C
To solve the problem step by step, we will find the measure of angle ADB in the rhombus ABCD given that angle ACB is 40 degrees.
1. Understanding the Properties of a Rhombus:
- In a rhombus, the diagonals bisect each other at right angles (90 degrees).
- Therefore, if we denote the intersection point of the diagonals as O, then angle AOD = 90 degrees.
Hint: Remember that the diagonals of a rhombus intersect at right angles.
2. Identifying Alternate Interior Angles:
- Since AB is parallel to CD and AC is a transversal, angle ACB (which is given as 40 degrees) is equal to angle DAO (alternate interior angles).
- Thus, we can write: angle DAO = angle ACB = 40 degrees.
Hint: Use the property of alternate interior angles when two parallel lines are cut by a transversal.
3. Using the Angle Sum Property in Triangle AOD:
- In triangle AOD, the sum of the angles is 180 degrees. Therefore, we can write:
angle DAO+angle AOD+angle ADB=180∘
- Substituting the known values, we have:
40∘+90∘+angle ADB=180∘
Hint: Recall that the sum of angles in any triangle is always 180 degrees.
4. Solving for angle ADB:
- Simplifying the equation:
130∘+angle ADB=180∘
- Now, subtract 130 degrees from both sides:
angle ADB=180∘−130∘=50∘
Hint: Perform basic arithmetic to isolate the variable you are solving for.
5. Conclusion:
- Therefore, the measure of angle ADB is 50 degrees.
Final Answer: angle ADB = 50 degrees.
- In a rhombus, the diagonals bisect each other at right angles (90 degrees).
- Therefore, if we denote the intersection point of the diagonals as O, then angle AOD = 90 degrees.
- Since AB is parallel to CD and AC is a transversal, angle ACB (which is given as 40 degrees) is equal to angle DAO (alternate interior angles).
- Thus, we can write: angle DAO = angle ACB = 40 degrees.
- In triangle AOD, the sum of the angles is 180 degrees. Therefore, we can write:
angle DAO+angle AOD+angle ADB=180∘
- Substituting the known values, we have:
40∘+90∘+angle ADB=180∘
- Simplifying the equation:
130∘+angle ADB=180∘
- Now, subtract 130 degrees from both sides:
angle ADB=180∘−130∘=50∘
- Therefore, the measure of angle ADB is 50 degrees.
Topper's Solved these Questions
- QUADRILATERALS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRILATERALS EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
14 Videos
- QUADRILATERALS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRILATERALS EXERCISE - SHORT ANSWER TYPE QUESTIONS
10 Videos
- POLYNOMIALSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - POLYNOMIALSEXERCISE - EXERCISE 2.4 Long Answer type Questions
9 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS
12 Videos
Similar Questions
Knowledge Check
A rhombus has :
Aone line of symmetryBtwo lines of symmetry eachCfour lines of symmetryDno line of symmetry
ABCD is a rhombus. If ∠BCA=35∘,and∠ADC.
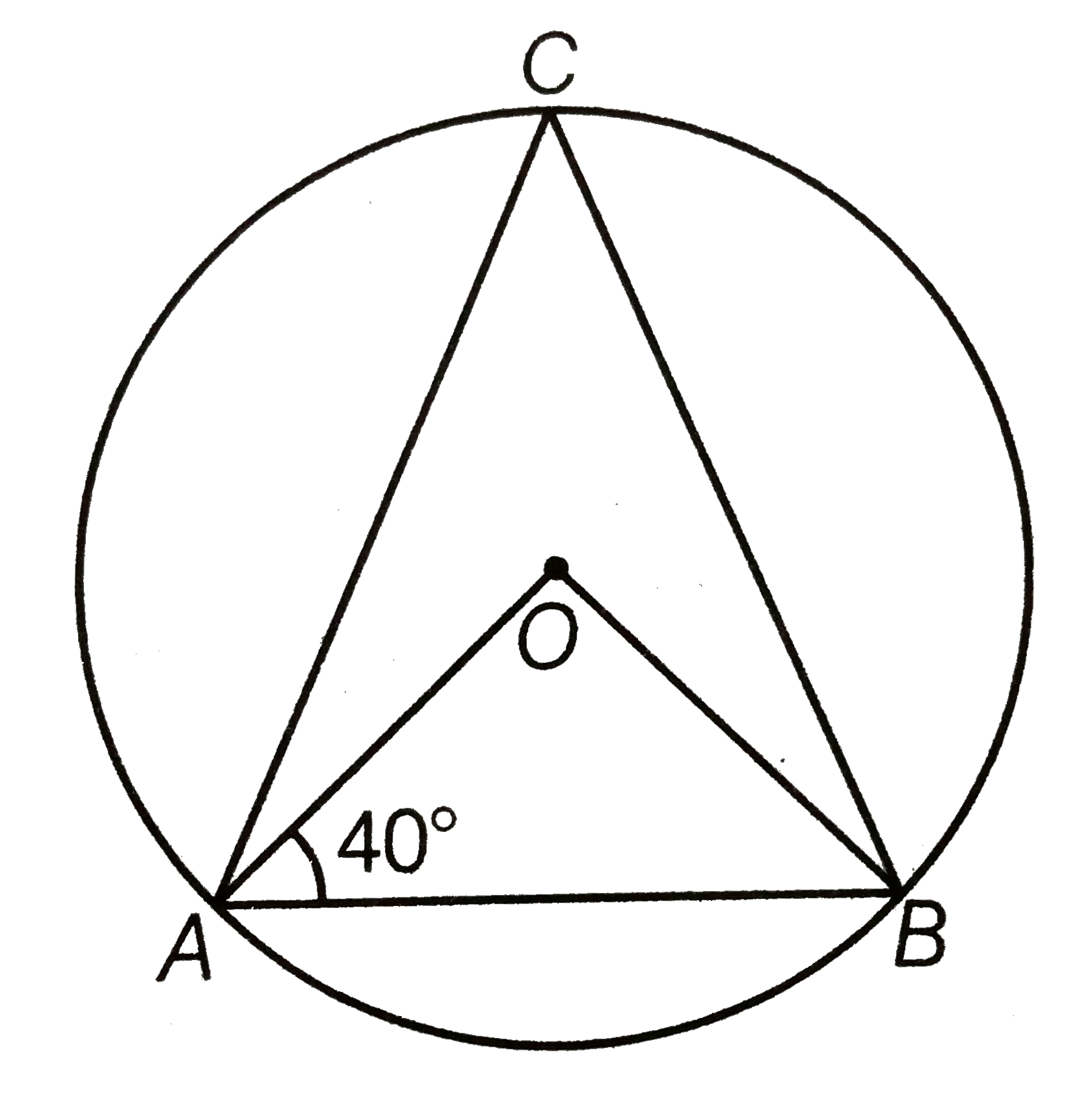
View SolutionIn figure, ∠ACB=40∘. Find ∠OAB.

View SolutionIn figure, if ∠OAB=40∘,then∠ACB is equal to
View SolutionABCD is a rhombus with ∠ABC=56∘, ∠BAC=62∘then ∠ACD is equal to:

View SolutionIn the given figure, ABCD is a rhombus with angle A=67∘
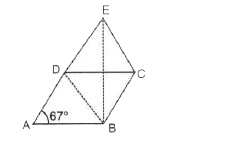
If DEC is an equilateral triangle, calculate:
∠CBE
View SolutionIn the given figure, ABCD is a rhombus with angle A = 67∘.
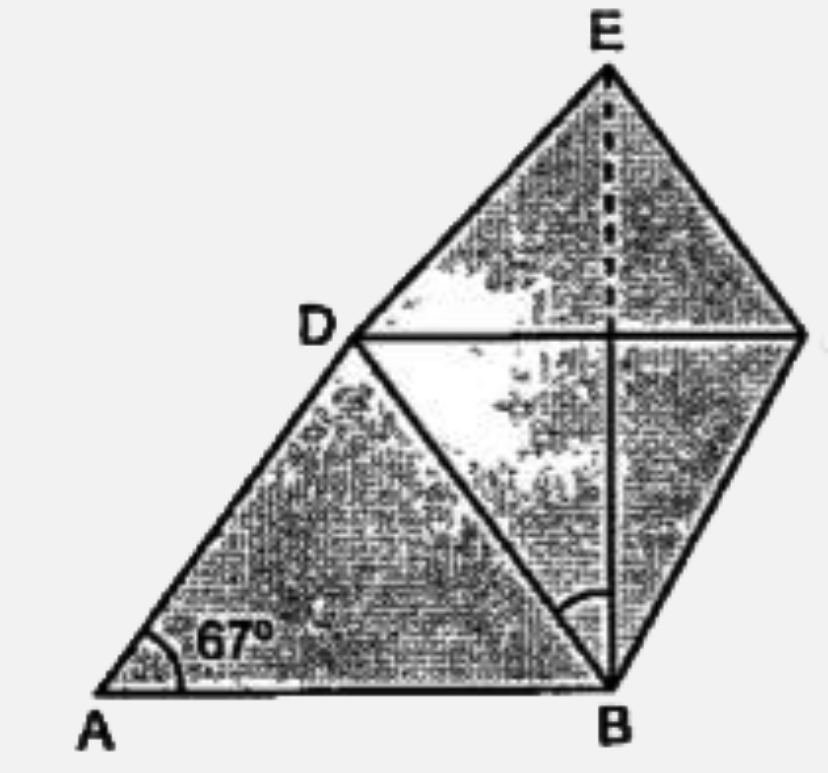
If DEC is an equilateral triangle. Calculate :
(i) ∠CBE (ii) ∠DBE
View SolutionIn the given figure, ABCD is a rhombus with angle A=67∘
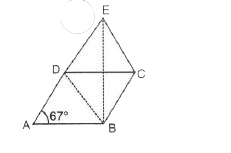
If DEC is an equilateral triangle, calculate:
∠DBE
View Solution