Question

Draw a neat labelled diagram of Young.s Double Slit experiment. Show that $\beta =\frac{\lambda D}{d}$, where the terms have their usual meaning (either for bright or dark fringe).

Explanation

Step-by-Step Solution

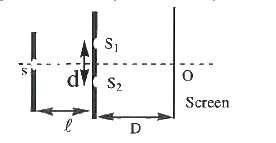
1. Draw the Diagram:
- Start by drawing a horizontal line to represent the screen.
- Mark the central maximum (C) at the center of the screen.
- Draw two narrow slits (S1 and S2) parallel to each other and above the screen. Label the distance between the slits as 'd'.
- Draw lines from S1 and S2 to a point P on the screen, which is at a distance 'x' from the central maximum (C).

2. Label the Distances:
- Label the distance from the slits to the screen as 'D'.
- Mark the distances from the central maximum (C) to the point P as 'x'.
- The distance from the center of the slits to the point P can be divided into two parts: \( CP = x \) and the distances from C to S1 and S2 as \( d/2 \).

3. Path Difference Calculation:
- The path difference (Δ) between the two waves reaching point P is given by:
\( Δ = S2P - S1P \)
- Using the right triangle properties, we can express S2P and S1P in terms of D and x:
- For S2P:
\( S2P^2 = D^2 + (x + d/2)^2 \)
- For S1P:
\( S1P^2 = D^2 + (x - d/2)^2 \)

4. Subtract the Two Equations:
- Subtract the equation for S1P from S2P:
\( S2P^2 - S1P^2 = (x + d/2)^2 - (x - d/2)^2 \)
- This simplifies to:
\( Δ = S2P - S1P = \frac{d \cdot x}{D} \)

5. Relate Path Difference to Fringe Width:
- For constructive interference (bright fringes), the path difference must equal \( n\lambda \):
\( Δ = n\lambda \)
- Setting the two expressions for Δ equal gives:
\( \frac{d \cdot x}{D} = n\lambda \)

6. Express Fringe Width (β):
- The fringe width (β) is defined as the distance between two consecutive bright fringes:
\( β = x_{n+1} - x_n \)
- From the previous equations, we can express:
\( x_n = \frac{n\lambda D}{d} \quad \text{and} \quad x_{n+1} = \frac{(n+1)\lambda D}{d} \)
- Therefore, the fringe width is:
\( β = \frac{(n+1)\lambda D}{d} - \frac{n\lambda D}{d} = \frac{\lambda D}{d} \)

Final Result
Thus, we conclude that the fringe width \( β \) is given by:
\( β = \frac{\lambda D}{d} \)