Starting with an expression for refraction at a single spherical surface, obtain Lens Maker.s formula.
Let a convex lens is taken which is made up of glass of refractive index n2. Let .O. is the point object placed on the principal axis and .u. is the distance of the object from P1.

For refraction at the first surface
n2v.−n1u=n2−n1R1 ......(1)
For refraction at the second surface
n1v−n2v.−t=n1−n2R2
If the lens is thin t<<<v., so
n1v−n1u=(n2−n1)(1R1−1R2)
Dividing both sides by n1, we get
1v−1u=(n2n1−1)(1R1−1R2)
Putting n2n1=n, we get
1v−1u=(n−1)(1R1−1R2)
When object is at infinity, image will be at focus
So, 1f−1∞=(n−1)(1R1−1R2)
1f=(n−1)(1R1−1R2)
This is lens maker.s formula
Similar Questions
Obtain an expression for refraction at a single convex spherical surface separating the two media having refractive indices μ1(rarer medium) and μ2(denser medium) i.e., a relation between u,v,μ1,μ2 and R.
View SolutionDerive an expression for refraction at a single (convex) spherical surface, i.e., a relation between u, v, R, n1 (rarer medium) and n2 (denser medium), where the terms have their usual meaning.
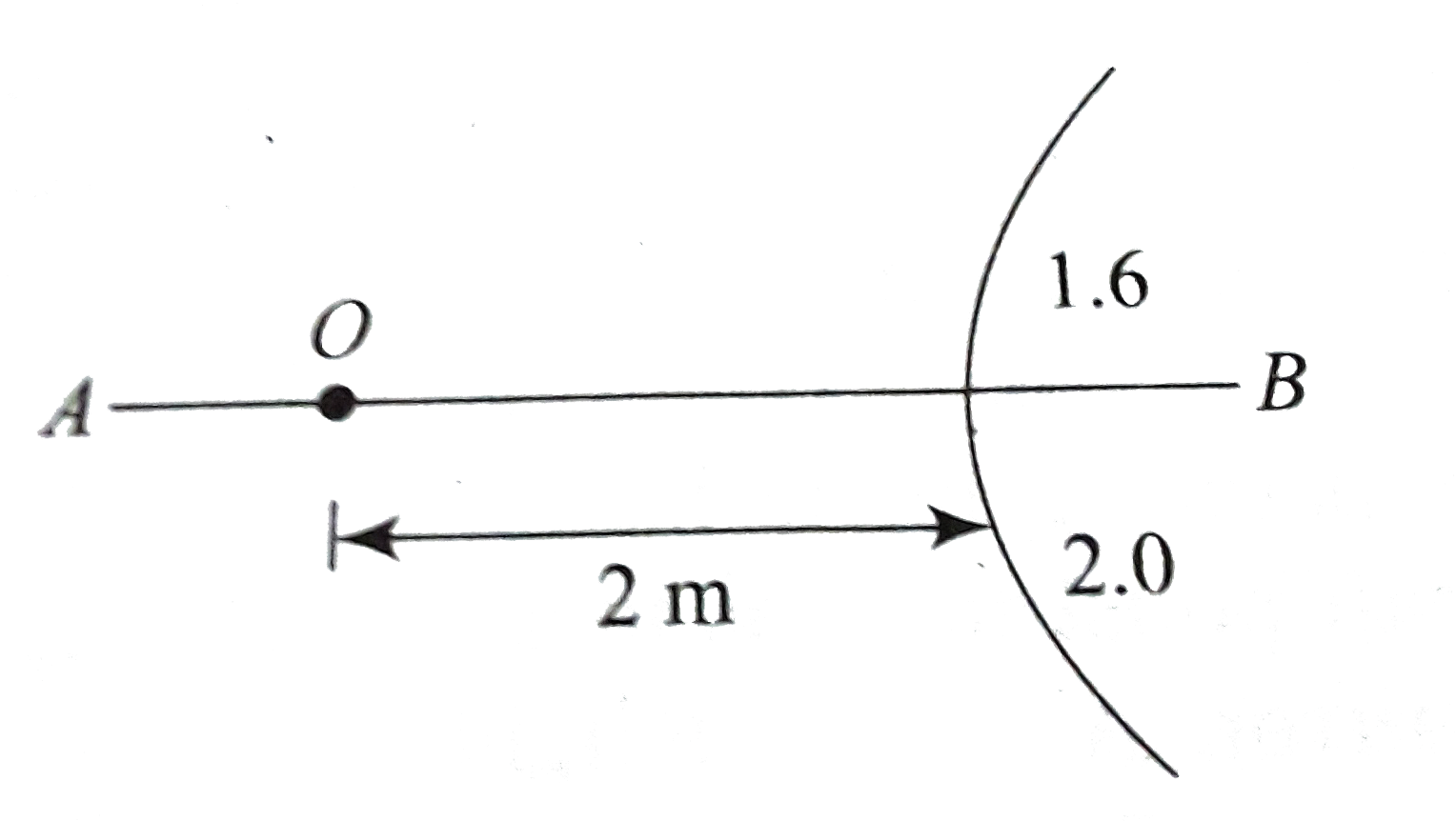
View SolutionIn Figure, a point object O is placed in air. A spherical boundary separates two media. Ab is the principall axis. The refractive index above AB is 1.6 and below AB is 2.0. The separation between the images formed due to refraction at a the spherical surface is (assume the radius of curvature (R) to be 1 unit)
View SolutionShow that for refraction at a concave spherical surface (separating glass-air medium), the distance of the object should be greater than three times the radius of curvature of the refracting surface for the image to be real.
View SolutionA person starts with a speed of √(0.5gr) at the top of a large frictionless spherical surface, and slides into the water below (see the drawing). Then , the person

View SolutionFigure below shows a parallel beam of monochromatic light incident on a convex spherical surface, radius of curvature R = 30 cm, which separates glass (refractive index - 1 6) from air. Find the position of the image formed due to refraction of light at this single spherical surface.

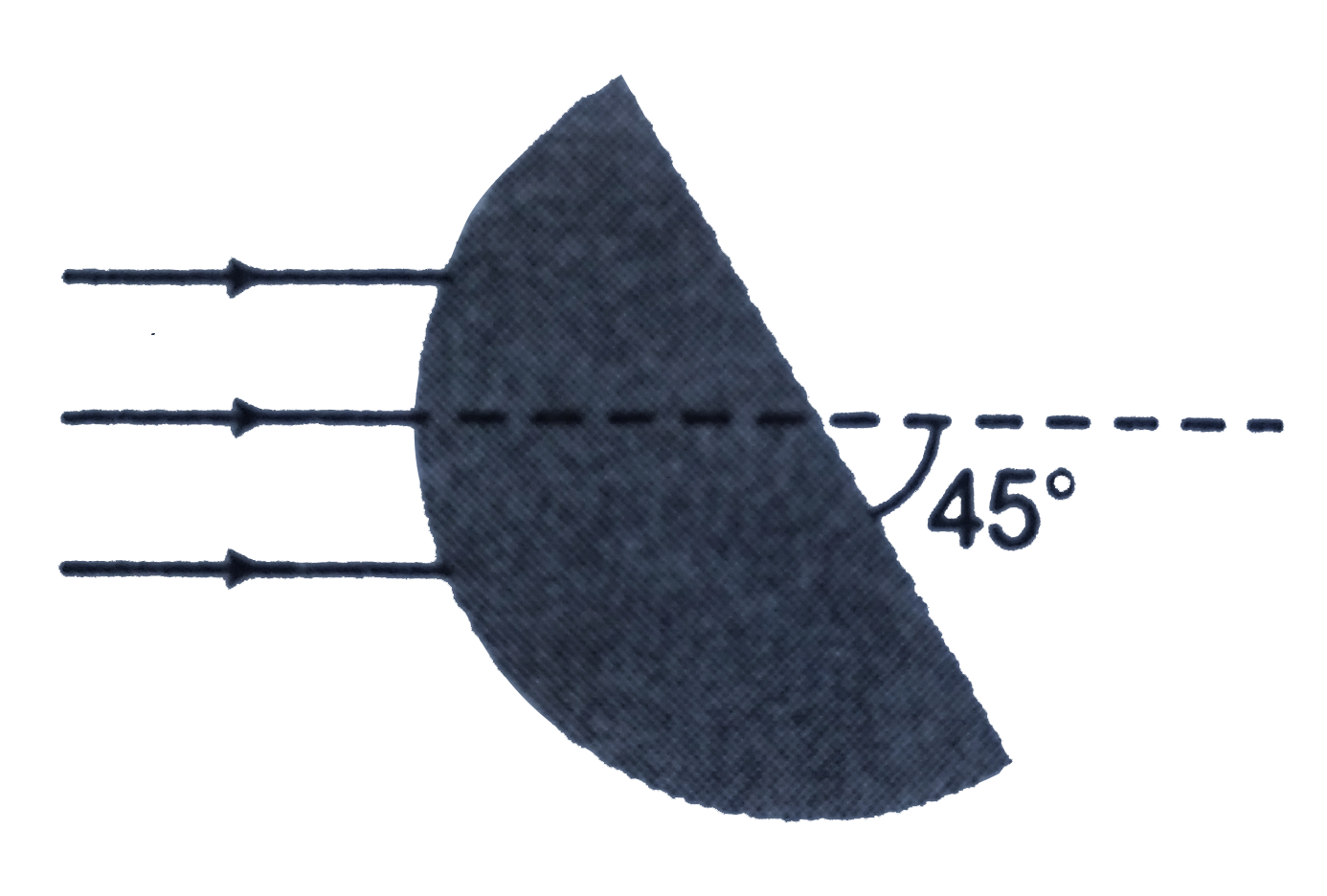
View SolutionA parallel narrow beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index μ=1.5 as shown. The position of the image formed by refraction at the image formed by refraction at the spherical surface only as
View SolutionHow is the refractive index of a medium related to the speed of light ? Obtain an expression for refractive index of a medium with respect to another in terms of speed of light in these two media ?
View SolutionTrace the rays of light showing the formation of an image due to a point object placed on the axis of a spherical surface separating the two media of refractive indices n1andn2. Establish the relation between the distance of the object, the image and the radius of curvature from the central point of the spherical surface.
Hence derive the expression of the lens maker's formula
View SolutionA ray of light is incident on a glass prism of refractive index μ and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence , angle of prism and critical angle.
View Solution