With the help of a neatly drawn and labelled diagram, obtain balancing condition of a Wheatstone bridge.
To derive the balancing condition of a Wheatstone bridge, we will follow these steps:
Step 1: Understand the Wheatstone Bridge Configuration
A Wheatstone bridge consists of four resistors arranged in a diamond shape. Label the points as follows:
- A and C are the two points connected to a voltage source.
- B and D are the two points connected to a galvanometer.
The resistors are labeled as:
- R1 between points A and B
- R2 between points B and C
- R3 between points D and C
- R4 between points A and D
Step 2: Define the Potentials
Let the potentials at points A, B, C, and D be:
- V_A at point A
- V_B at point B
- V_C at point C
- V_D at point D
Step 3: Apply Ohm's Law
Using Ohm's law, we can express the potential differences across the resistors:
1. The potential difference across R1 is given by:
VA−VB=I1⋅R1(Equation 1)
2. The potential difference across R2 is given by:
VB−VC=(I1+IG)⋅R2(Equation 2)
3. The potential difference across R4 is given by:
VA−VD=(I−I1−IG)⋅R4(Equation 3)
4. The potential difference across R3 is given by:
VD−VC=(I−I1)⋅R3(Equation 4)
Step 4: Condition for Balance
The bridge is said to be balanced when no current flows through the galvanometer (I_G = 0). Under this condition, we can simplify the equations:
- From Equation 1 and Equation 3:
VA−VB=VA−VD
This simplifies to:
I1R1=(I−I1)R4(Equation 5)
- From Equation 2 and Equation 4:
VB−VC=VD−VC
This simplifies to:
I1R2=(I−I1)R3(Equation 6)
Step 5: Derive the Balancing Condition
Dividing Equation 5 by Equation 6 gives:
I1R1I1R2=(I−I1)R4(I−I1)R3
This simplifies to:
R1R2=R3R4
This is the required balancing condition for the Wheatstone bridge.
Step 6: Draw the Diagram
Draw a neat diagram of the Wheatstone bridge, labeling all points (A, B, C, D) and resistors (R1, R2, R3, R4) clearly. Indicate the direction of current flow and the galvanometer connection.
A Wheatstone bridge consists of four resistors arranged in a diamond shape. Label the points as follows:
- A and C are the two points connected to a voltage source.
- B and D are the two points connected to a galvanometer.
- R1 between points A and B
- R2 between points B and C
- R3 between points D and C
- R4 between points A and D
Let the potentials at points A, B, C, and D be:
- V_A at point A
- V_B at point B
- V_C at point C
- V_D at point D
Using Ohm's law, we can express the potential differences across the resistors:
1. The potential difference across R1 is given by:
VA−VB=I1⋅R1(Equation 1)
2. The potential difference across R2 is given by:
VB−VC=(I1+IG)⋅R2(Equation 2)
3. The potential difference across R4 is given by:
VA−VD=(I−I1−IG)⋅R4(Equation 3)
4. The potential difference across R3 is given by:
VD−VC=(I−I1)⋅R3(Equation 4)
The bridge is said to be balanced when no current flows through the galvanometer (I_G = 0). Under this condition, we can simplify the equations:
- From Equation 1 and Equation 3:
VA−VB=VA−VD
This simplifies to:
I1R1=(I−I1)R4(Equation 5)
VB−VC=VD−VC
This simplifies to:
I1R2=(I−I1)R3(Equation 6)
Dividing Equation 5 by Equation 6 gives:
I1R1I1R2=(I−I1)R4(I−I1)R3
This simplifies to:
R1R2=R3R4
This is the required balancing condition for the Wheatstone bridge.
Draw a neat diagram of the Wheatstone bridge, labeling all points (A, B, C, D) and resistors (R1, R2, R3, R4) clearly. Indicate the direction of current flow and the galvanometer connection.
Similar Questions
With the help of a labelled diagram, show that the balancing condition of a Wheatstone bridge is : R1R2=R3R4 where the terms have their usual meaning.
View SolutionWith the help of a neatly drawn labelled diagram, prove that the magnitude of motional emf .e. is given by e=Blv, where .I. is the length of a metallic rod and v is the velocity with which it is pulled in a transverse magnetic field .B..
View SolutionExplain meiosis with the help of labelled diagrams.
View SolutionWith the help of labelled diagrams show the mechanism of beathing in humans.
View SolutionDraw a neat labelled diagram of Young.s Double Slit experiment. Show that β=λDd, where the terms have their usual meaning (either for bright or dark fringe).
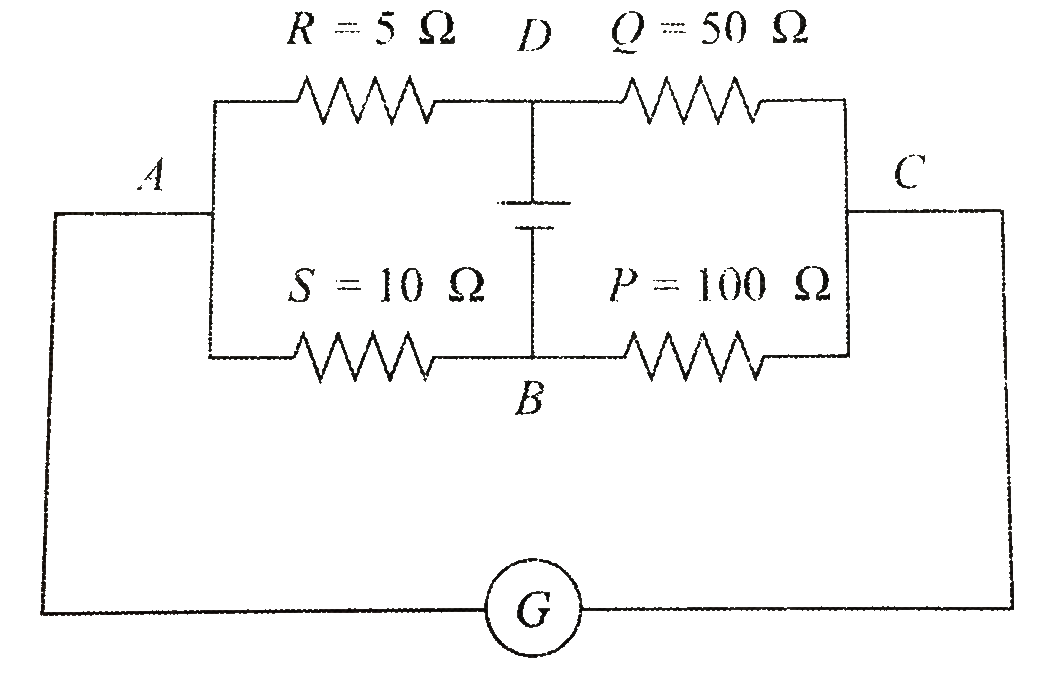
View SolutionFigure 6.64 shows a balanced wheatstone bridge.
View SolutionExplain briefly, with the help of a neat labelled diagram, how does white light get dispersed by a prism.
On which surface of a prism, there is both dispersion and deviation of light, and on which surface of the prism, there is only deviation of light?
View SolutionWrite an expression for the force experienced by the charged particle moving in a uniform magnetic field B. With the help of labeled diagram explain the working of cyclotron. Show that cyclotron frequency does not depend upon the speed of the particle.
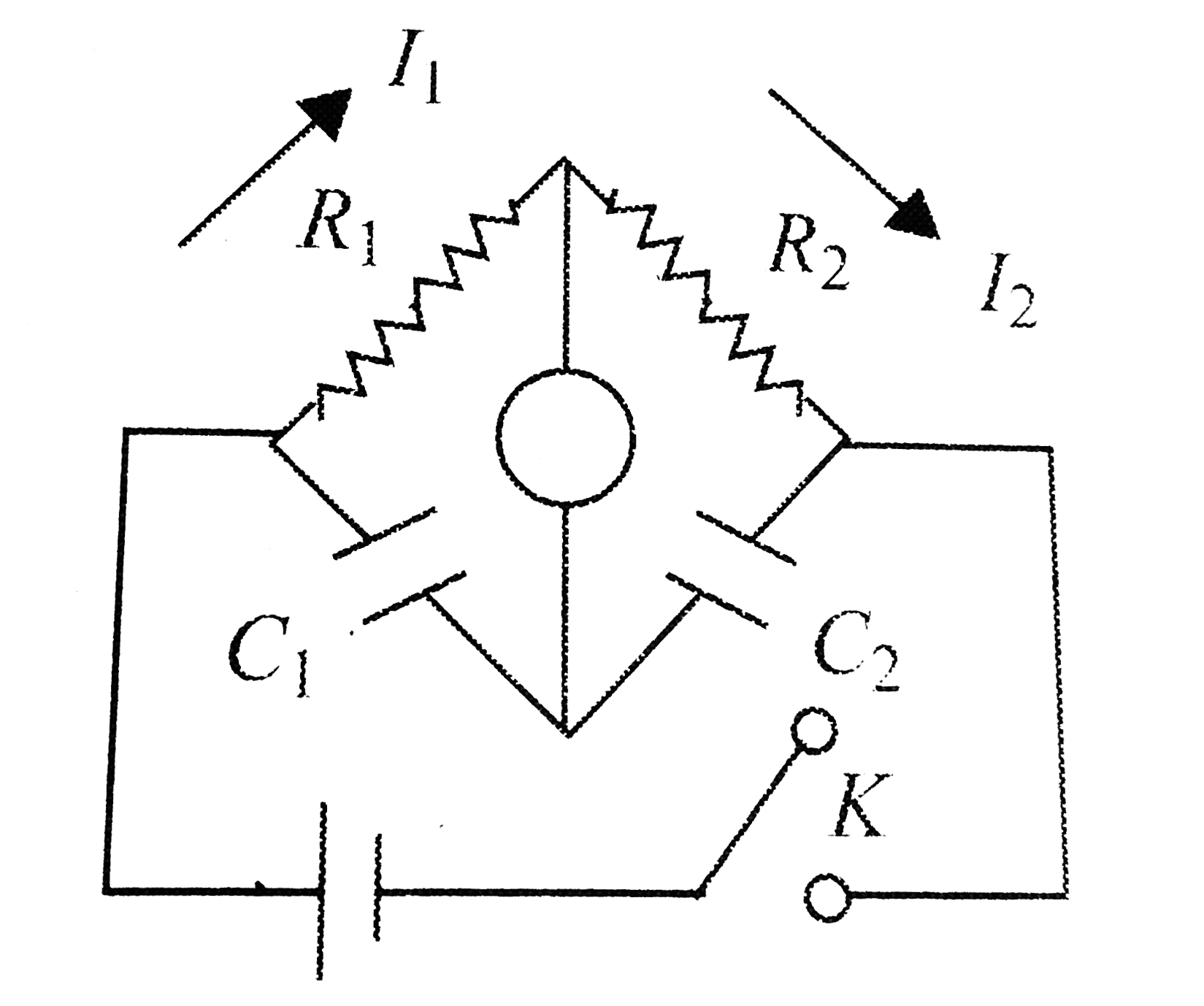
View SolutionIn the circuit in fig. If no current flows through the galvanometer when the key k is closed, the bridge is balanced. The balancing condition for bridge is
View SolutionWith the help of a labelled diagram, explain why the sun appears reddish at the sunrise and the sunset.
View Solution

