If earth is 1/4 of its present distance formt he sun, then what is the duration of the year?
The correct Answer is:0.125years
To solve the problem of finding the duration of the year if the Earth is at 14 of its present distance from the Sun, we can use Kepler's Third Law of planetary motion. This law states that the square of the period of revolution (T) of a planet is directly proportional to the cube of the semi-major axis (R) of its orbit around the Sun.
1. Identify the Variables:
- Let T1 be the current period of the Earth (1 year).
- Let R1 be the current distance from the Earth to the Sun (1 astronomical unit, AU).
- Let T2 be the new period we want to find.
- Let R2 be the new distance from the Earth to the Sun, which is 14R1.
2. Apply Kepler's Third Law:
According to Kepler's Third Law:
T21T22=R31R32
3. Substituting Known Values:
We know T1=1 year and R2=14R1. Therefore:
R2=14R1
Thus, we can express R32:
R32=(14R1)3=164R31
4. Setting Up the Equation:
Substitute R32 into the equation:
12T22=R31164R31
Simplifying gives:
1T22=64
5. Solving for T22:
Taking the reciprocal:
T22=164
6. Finding T2:
Taking the square root:
T2=18 years
Final Answer:
The duration of the year when the Earth is 14 of its present distance from the Sun is 18 years.
---
- Let T1 be the current period of the Earth (1 year).
- Let R1 be the current distance from the Earth to the Sun (1 astronomical unit, AU).
- Let T2 be the new period we want to find.
- Let R2 be the new distance from the Earth to the Sun, which is 14R1.
According to Kepler's Third Law:
T21T22=R31R32
We know T1=1 year and R2=14R1. Therefore:
R2=14R1
Thus, we can express R32:
R32=(14R1)3=164R31
Substitute R32 into the equation:
12T22=R31164R31
Simplifying gives:
1T22=64
Taking the reciprocal:
T22=164
Taking the square root:
T2=18 years
The duration of the year when the Earth is 14 of its present distance from the Sun is 18 years.
Topper's Solved these Questions
- GRAVITATIONBook:ICSEChapter:GRAVITATIONExercise:FROM THE HUBBLE TELESCOP
Explore 2 Videos
- GRAVITATIONBook:ICSEChapter:GRAVITATIONExercise:SELECTED PROBLEMS[FROM ESCAPE VELOCITY ]
Explore 20 Videos
- FRICTIONBook:ICSEChapter:FRICTIONExercise:Selected problems
Explore 30 Videos
- INTERNAL ENERGY Book:ICSEChapter:INTERNAL ENERGY Exercise:SELECTED PROBLEMS (FROM HEAT ENGINES)
Explore 21 Videos
Similar Questions
If the earth be one-half of its present distance from the sun, how many days will be in one year ?
View SolutionIf radius of the earth contracts to half of its present value without change in its mass, what will be the new duration of the day?
View SolutionIf the radius of the earth contracts to half of its present value without change in its mass, what will be the new duration of the day?
View SolutionIf the radius of the earth contracts to half of its present value without change in its mass, what will be the new duration of the day?
View SolutionIf radius of the earth contracts to half of its present value without change in its mass, what will be the new duration of the day?
View SolutionThe radiations emitted by the sun are analyzeed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
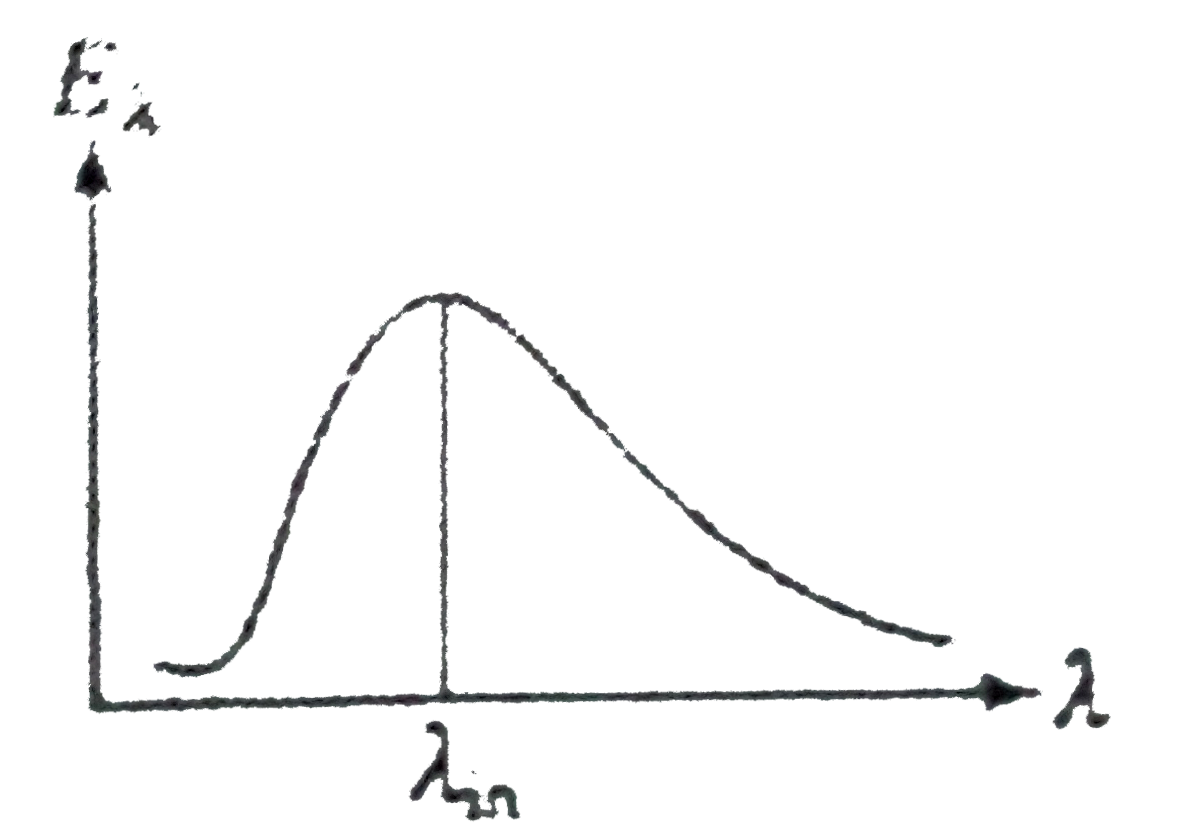
If the earth is at a distance 'd' from the sun the intensity of light falling on the earth (called solar constant S) is
View SolutionThe largest and the shortest distance of the earth from the sun are r1 and r2, its distance from the sun when it is at the perpendicular to the major axis of the orbit drawn from the sun
View SolutionIf the earth, were suddenly contracted to (l/n)th of its present radius without change in its mass, then what will be the effect on the duration of the day.
View SolutionThe time period of earth is taken as T and its distance from sun as R. What will be the distance of a certain planet from sun whose time period is 64 times that of earth ?
View SolutionThe time period of earth is taken as T and its distance from sun as R. What will be the distance of a certain planet from sun whose time period is 64 times that of earth ?
View Solution

