Find the magnitude of angle A, if :
The correct Answer is:
To solve the equation sin2(2x)+sin2(60∘)=1, we will follow these steps:
Step 1: Substitute the value of sin(60∘)
We know that:
sin(60∘)=√32
Thus, we can calculate sin2(60∘):
sin2(60∘)=(√32)2=34
Step 2: Rewrite the equation
Now, substitute sin2(60∘) into the original equation:
sin2(2x)+34=1
Step 3: Isolate sin2(2x)
To isolate sin2(2x), subtract 34 from both sides:
sin2(2x)=1−34
sin2(2x)=14
Step 4: Take the square root
Now, take the square root of both sides:
sin(2x)=±12
Step 5: Find the angles for sin(2x)=12
The angles for which sin(θ)=12 are:
2x=30∘+n⋅360∘or2x=150∘+n⋅360∘(n∈Z)
Step 6: Solve for x
Dividing by 2, we get:
1. x=15∘+n⋅180∘
2. x=75∘+n⋅180∘
Step 7: Consider the principal value
For the principal value, we can take n=0:
- From the first equation: x=15∘
- From the second equation: x=75∘
Conclusion
The possible values for x are 15∘ and 75∘.
We know that:
sin(60∘)=√32
Thus, we can calculate sin2(60∘):
sin2(60∘)=(√32)2=34
Now, substitute sin2(60∘) into the original equation:
sin2(2x)+34=1
To isolate sin2(2x), subtract 34 from both sides:
sin2(2x)=1−34
sin2(2x)=14
Now, take the square root of both sides:
sin(2x)=±12
The angles for which sin(θ)=12 are:
2x=30∘+n⋅360∘or2x=150∘+n⋅360∘(n∈Z)
Dividing by 2, we get:
1. x=15∘+n⋅180∘
2. x=75∘+n⋅180∘
For the principal value, we can take n=0:
- From the first equation: x=15∘
- From the second equation: x=75∘
The possible values for x are 15∘ and 75∘.
Topper's Solved these Questions
- TRIGONOMETRICAL RATIOS OF STANDARD ANGLESBOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS OF STANDARD ANGLESEXERCISE - EXERCISE 23(A)
68 Videos
- TRIGONOMETRICAL RATIOS OF STANDARD ANGLESBOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS OF STANDARD ANGLESEXERCISE - EXERCISE 23(B)
34 Videos
- TRIGONOMETRICAL RATIOS BOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - EXERCISE 22(B)
50 Videos
- TRIGONOMETRYBOOK - ICSECHAPTER - TRIGONOMETRYEXERCISE - TOPIC -4 ( COMPLEMENTARY ANGLES ) (4 MARKS QUESTIONS )
4 Videos
Similar Questions
Find the magnitude of angle A, if :
sin22A+sin260∘=1
View SolutionFind the magnitude of angle A, if :
2sin2A−3sinA+1=0
View SolutionFind the value of angle A , if :
2 sin A=1
View SolutionFind the value of angle A , if :
2 sin 2A =1
View SolutionFind the value of angle A , if :
sin 2A = 1
View SolutionFind the magnitude of angle A, if :
4sinAsin2A+1−2sin2A=2sinA
View SolutionFind the value of :
cos260∘+sin230∘
View SolutionFind the value of :
cos260∘+sin230∘
View Solutionfind the maximum value of f(x)=(sin−1(sinx))2−sin−1(sinx)
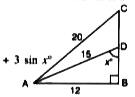
View SolutionIn the given figure ∠B=90∘and∠ADB=x∘, Find :
(i) sin∠CAB
(ii)cos2C∘+sin2C∘
(iii) tanx∘−cosx∘+3sinx∘
View Solution
