In rectangle ABCD, diagonal BD = 26 cm and cotangent of angle ABD = 1.5. Find the area and the perimeter of the rectangle ABCD.
The correct Answer is:Area = 312 sq . Cm and perimeter =20√13 cm
To solve the problem step by step, we will use the information given about rectangle ABCD, the diagonal BD, and the cotangent of angle ABD.
Step 1: Understand the Given Information
We have a rectangle ABCD with diagonal BD = 26 cm and cotangent of angle ABD = 1.5. We need to find the area and perimeter of the rectangle.
Step 2: Draw the Rectangle
Draw rectangle ABCD and label the corners A, B, C, and D. The diagonal BD divides the rectangle into two right triangles, ABD and BCD.
Step 3: Define the Angles and Sides
Let:
- L = length of rectangle (AB)
- B = breadth of rectangle (AD)
- θ = angle ABD
Given:
- cotθ=1.5
Step 4: Use the Cotangent Definition
The cotangent of an angle is defined as:
cotθ=AdjacentOpposite=LB
From the given cotangent value:
LB=1.5orL=1.5B
Step 5: Use the Diagonal Length
In triangle ABD, we can apply the Pythagorean theorem:
BD2=AB2+AD2
Substituting the known values:
262=L2+B2
676=L2+B2
Step 6: Substitute for Length
Substituting L=1.5B into the Pythagorean theorem:
676=(1.5B)2+B2
676=2.25B2+B2
676=3.25B2
Step 7: Solve for Breadth
Now, solve for B2:
B2=6763.25
Calculating this gives:
B2=208
Taking the square root:
B=√208=4√13cm
Step 8: Find Length
Now substitute back to find L:
L=1.5B=1.5×4√13=6√13cm
Step 9: Calculate Area
The area A of the rectangle is given by:
A=L×B=(6√13)×(4√13)=24×13=312cm2
Step 10: Calculate Perimeter
The perimeter P of the rectangle is given by:
P=2(L+B)=2(6√13+4√13)=2(10√13)=20√13cm
Final Answers
- Area = 312cm2
- Perimeter = 20√13cm
We have a rectangle ABCD with diagonal BD = 26 cm and cotangent of angle ABD = 1.5. We need to find the area and perimeter of the rectangle.
Draw rectangle ABCD and label the corners A, B, C, and D. The diagonal BD divides the rectangle into two right triangles, ABD and BCD.
Let:
- L = length of rectangle (AB)
- B = breadth of rectangle (AD)
- θ = angle ABD
- cotθ=1.5
The cotangent of an angle is defined as:
cotθ=AdjacentOpposite=LB
From the given cotangent value:
LB=1.5orL=1.5B
In triangle ABD, we can apply the Pythagorean theorem:
BD2=AB2+AD2
Substituting the known values:
262=L2+B2
676=L2+B2
Substituting L=1.5B into the Pythagorean theorem:
676=(1.5B)2+B2
676=2.25B2+B2
676=3.25B2
Now, solve for B2:
B2=6763.25
Calculating this gives:
B2=208
Taking the square root:
B=√208=4√13cm
Now substitute back to find L:
L=1.5B=1.5×4√13=6√13cm
The area A of the rectangle is given by:
A=L×B=(6√13)×(4√13)=24×13=312cm2
The perimeter P of the rectangle is given by:
P=2(L+B)=2(6√13+4√13)=2(10√13)=20√13cm
- Area = 312cm2
- Perimeter = 20√13cm
Topper's Solved these Questions
- TRIGONOMETRICAL RATIOS Book:ICSEChapter:TRIGONOMETRICAL RATIOS Exercise:EXERCISE 22(A)
Explore 47 Videos
- TRIANGLES Book:ICSEChapter:TRIANGLES Exercise:4 MARKS QUESTIONS
Explore 24 Videos
- TRIGONOMETRICAL RATIOS OF STANDARD ANGLESBook:ICSEChapter:TRIGONOMETRICAL RATIOS OF STANDARD ANGLESExercise:EXERCISE 23(C)
Explore 118 Videos
Similar Questions
Knowledge Check
AC, a diagnonal of the rectange ABCD , measure 5 units. The area of the rectangle is 12 sq. units. What is the perimeter of the rectangle?
A7B14C17D20
In rhombus ABCD , diagonal AC = 18 cm , the angle between diagonal BD and side AB is α such that cosα=0.8. Find the diagonal BD and the perimeter of rhombus ABCD.
View SolutionA square and a rectangle have equal area. If side of a square is 24 cm and the length of the rectangle is 32 cm , find
the perimeter of the rectangle.
View SolutionThe measurements of the sides of a rectangle are given. Find
(i) the value of x.
(ii) the area of the rectangle
(iii) the perimeter of the rectangle .
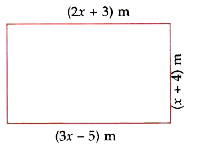
View SolutionIf a rectangle has breadth 11 m and area 264 sq. m, what is the length of the rectangle? Also, find the perimeter of the rectangle.
View SolutionThe area of a square and a rectangle are equal.If the side of the square is 40 cm and the breadth of the rectangle is 25 cm,find the length of the rectangle. Also,find the perimeter of the rectangle.
View SolutionThe area of a square and a rectangle are equal. If the side of the square is40 cm and the breadth of the rectangle is 25 cm, find the length of therectangle. Also, find the perimeter of the rectangle.
View SolutionContruct a rectangle ABCD with diagonal AC = 6.6 cm , side BC = 5.2 cm and ∠B=60∘
View Solution

