In triangle ABC, AD is perpendicular to BC. sin B = 0.8, BD = 9 cm and tan C = 1. Find the length of AB, AD, AC and DC.
The correct Answer is:Taking BD = 9 cm , we get : AB = 15 cm, AD = 12 cm , AC = 12√2cmandDC=12cm
Step by step video, text & image solution for In triangle ABC, AD is perpendicular to BC. sin B = 0.8, BD = 9 cm and tan C = 1. Find the length of AB, AD, AC and DC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIGONOMETRICAL RATIOS Book:ICSEChapter:TRIGONOMETRICAL RATIOS Exercise:EXERCISE 22(A)
Explore 47 Videos
- TRIANGLES Book:ICSEChapter:TRIANGLES Exercise:4 MARKS QUESTIONS
Explore 24 Videos
- TRIGONOMETRICAL RATIOS OF STANDARD ANGLESBook:ICSEChapter:TRIGONOMETRICAL RATIOS OF STANDARD ANGLESExercise:EXERCISE 23(C)
Explore 118 Videos
Similar Questions
In triangle ABC,AD is perpendicular to side BC and AD2=BD×DC.
Show that angle BAC=90∘.
View SolutionIn triangles ABC , AD is perpendicular to BC and AD2=BD×DC . Prove that angle BAC=90∘
View SolutionIn Triangle ABC, AD is perpendicular to BC, tanB=34tanC=512 and BC = 56 cm . Calculate the lengths of AD.
View SolutionABC is a right angled triangle with ∠ABC=90∘, D is any point on AB and DE is perpendicular to AC.
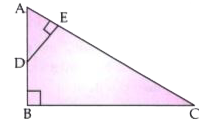
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
View SolutionIn a ΔABC, the median AD is perpendicular to AC. If b = 5 and c = 11, then a =
View SolutionΔABC is right-angled at C. If AC=5cmandBC=12cm find the length of AB.
View SolutionIn the figure, AD is perpendicular to BC, prove that AB+AC>2AD.

View SolutionIn DetlaABC,AD is perpendicular to BC. If AD = 12 cm, area of ΔADB=90sq.cm. and area of DetlaADB: area De≤taADC=2:3, find BD and DC.

View SolutionIn Figure -6 , in an equilateral triangle ABC, AD is perpendicular to BC , BE is perpendicular to AC and CF is perpendicular to AB . Prove that 4(AD2+BE2+CF2)=9AB2
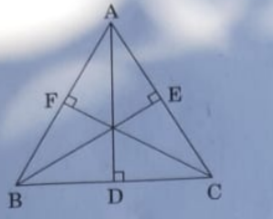
View SolutionIn ΔABC, the perependicular from A BC meets BC at D such that BD=7cmandDC=12cm.Find the ratio of the areas of the triangles ABD and ADC.
View Solution

