In a pentagon ABCDE, AB is parallel to DC and ∠A:∠E:∠D=3:4:5. Find angle E.
The correct Answer is:120∘
To solve the problem, we need to find the measure of angle E in the pentagon ABCDE, given that AB is parallel to DC and the angles are in the ratio 3:4:5.
1. Understand the Geometry:
- We have a pentagon ABCDE where AB is parallel to DC.
- Since AB is parallel to DC, angles B and C are both right angles (90 degrees).
2. Set Up the Ratio of Angles:
- We are given that the angles A, E, and D are in the ratio 3:4:5.
- Let angle A = 3k, angle E = 4k, and angle D = 5k.
3. Sum of Interior Angles of a Pentagon:
- The formula for the sum of interior angles of a polygon is (n - 2) × 180 degrees, where n is the number of sides.
- For a pentagon (n = 5), the sum of the interior angles = (5 - 2) × 180 = 3 × 180 = 540 degrees.
4. Write the Equation for the Angles:
- The sum of the angles in the pentagon can be expressed as:
Angle A+Angle B+Angle C+Angle D+Angle E=540
- Substituting the known angles:
3k+90+90+5k+4k=540
5. Combine Like Terms:
- Combine the terms involving k:
3k+5k+4k+180=540
12k+180=540
6. Isolate k:
- Subtract 180 from both sides:
12k=540−180
12k=360
- Divide both sides by 12:
k=30
7. Find Angle E:
- Now substitute k back to find angle E:
Angle E=4k=4×30=120
Final Answer:
- Angle E = 120 degrees.
- We have a pentagon ABCDE where AB is parallel to DC.
- Since AB is parallel to DC, angles B and C are both right angles (90 degrees).
- We are given that the angles A, E, and D are in the ratio 3:4:5.
- Let angle A = 3k, angle E = 4k, and angle D = 5k.
- The formula for the sum of interior angles of a polygon is (n - 2) × 180 degrees, where n is the number of sides.
- For a pentagon (n = 5), the sum of the interior angles = (5 - 2) × 180 = 3 × 180 = 540 degrees.
- The sum of the angles in the pentagon can be expressed as:
Angle A+Angle B+Angle C+Angle D+Angle E=540
- Substituting the known angles:
3k+90+90+5k+4k=540
- Combine the terms involving k:
3k+5k+4k+180=540
12k+180=540
- Subtract 180 from both sides:
12k=540−180
12k=360
- Divide both sides by 12:
k=30
- Now substitute k back to find angle E:
Angle E=4k=4×30=120
- Angle E = 120 degrees.
Topper's Solved these Questions
- RECTILINEAR FIGURESBOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - Exercise 14(B) (true/false)
10 Videos
- RECTILINEAR FIGURESBOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - Exercise 14(B)
16 Videos
- RECTILINEAR FIGURESBOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - QUADRILATERALS AND ITS PROPERTIES - 4 MARKS QUESTIONS
7 Videos
- RATIONAL AND IRRATIONAL NUMBERS BOOK - ICSECHAPTER - RATIONAL AND IRRATIONAL NUMBERS EXERCISE - EXERCISE 1 (D)
21 Videos
- SIMULTANEOUS EQUATIONSBOOK - ICSECHAPTER - SIMULTANEOUS EQUATIONSEXERCISE - EXERCISE 6 (G)
13 Videos
Similar Questions
In a hexagon, ABCDEF, side AB is parallel to side FE and ∠B:∠C:∠D:∠E=6:4:2:3 Find ∠Band∠D.
View SolutionIn a pentagon ABCDE, AB is parallel to ED and angle B=140∘. Find the angles C and D, if ∠C:∠D=5:6
View SolutionIn quadrilateral ABCD, side AB is parallel to side DC. If ∠A:∠D=1:2and∠C:∠B=4:5.
(i) Calculate each angle of the quadrilateral.
(ii) Assign a special name to quadrialateral ABCD.
View SolutionThe figure, given below, shows a pentagon ABCDE with sides AB and ED parallel to each other, and ∠B:∠C:∠D=5:6:7.
(i) Using formula, find the sum of interior angles of the pentagon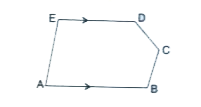
(ii) Write the value of ∠A+∠E.
(iii) Find angles B,C and D
View SolutionFind ∠A+∠B+∠C+∠D
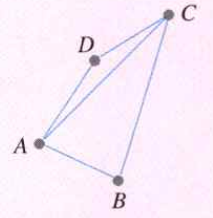
View SolutionThe following figure shows a quadrilateral in which sideo AB and DC are parallel. If ∠A:∠D=4:5,∠B=(3x−15)∘and∠C=(4x+20)∘, find each angle of the quadrilateral ABCD.

View SolutionIn the given figure,AB is parallel to DC. ∠BCE=80∘and∠BAC=25∘.F∈d:(i) angle CAD <br>(ii) angle CBD <br>(iii) angle ADC
View SolutionABCDE is a pentagon in which AB = AE, BC = ED and ∠ABC=∠AED.
Prove that
AC= AD
(ii) ∠BCD=∠EDC
View SolutionIn a regular pentagon ABCDE inscribed in a circle . Find the ratio between angle ADE and angle ADC.
View SolutionIn a cyclic quadrilateral ABCD ∠A:∠C=3:1and angle B : angle D = 1 : 5 find each angle of the quadrilateral
View Solution
