In a regular pentagon ABCDE inscribed in a circle . Find the ratio between angle ADE and angle ADC.
The correct Answer is:1:2:7,(i)24∘(ii)72∘(iii)48∘
To solve the problem of finding the ratio between angle ADE and angle ADC in a regular pentagon ABCDE inscribed in a circle, we can follow these steps:
1. Understanding the Pentagon:
- We have a regular pentagon ABCDE inscribed in a circle. In a regular pentagon, all sides and angles are equal.
2. Drawing the Diagram:
- Draw a circle and inscribe the pentagon ABCDE. Mark the center of the circle as O.
3. Calculating Central Angles:
- The total angle around point O (the center of the circle) is 360 degrees. Since the pentagon has 5 equal angles at the center, each central angle (like angle AOE) can be calculated as:
Angle AOE=360∘5=72∘
4. Finding Angle ADE:
- Angle ADE is subtended by arc AE at the circumference. The angle subtended at the circumference is half of the angle subtended at the center. Therefore:
Angle ADE=12×Angle AOE=12×72∘=36∘
5. Finding Angle ADC:
- Angle ADC is the sum of angles ADB and BDC. Since both angles are subtended by the arcs AB and BC respectively, and each subtended angle at the circumference is also 36 degrees:
Angle ADB=36∘andAngle BDC=36∘
- Thus, we can calculate angle ADC as:
Angle ADC=Angle ADB+Angle BDC=36∘+36∘=72∘
6. Finding the Ratio:
- Now, we can find the ratio of angle ADE to angle ADC:
Ratio=Angle ADEAngle ADC=36∘72∘=12
7. Final Answer:
- Therefore, the ratio of angle ADE to angle ADC is:
Angle ADE : Angle ADC=1:2
- We have a regular pentagon ABCDE inscribed in a circle. In a regular pentagon, all sides and angles are equal.
- Draw a circle and inscribe the pentagon ABCDE. Mark the center of the circle as O.
- The total angle around point O (the center of the circle) is 360 degrees. Since the pentagon has 5 equal angles at the center, each central angle (like angle AOE) can be calculated as:
Angle AOE=360∘5=72∘
- Angle ADE is subtended by arc AE at the circumference. The angle subtended at the circumference is half of the angle subtended at the center. Therefore:
Angle ADE=12×Angle AOE=12×72∘=36∘
- Angle ADC is the sum of angles ADB and BDC. Since both angles are subtended by the arcs AB and BC respectively, and each subtended angle at the circumference is also 36 degrees:
Angle ADB=36∘andAngle BDC=36∘
- Thus, we can calculate angle ADC as:
Angle ADC=Angle ADB+Angle BDC=36∘+36∘=72∘
- Now, we can find the ratio of angle ADE to angle ADC:
Ratio=Angle ADEAngle ADC=36∘72∘=12
- Therefore, the ratio of angle ADE to angle ADC is:
Angle ADE : Angle ADC=1:2
Topper's Solved these Questions
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )
28 Videos
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(A)
58 Videos
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (PROBABILITY)
16 Videos
- CONSTRUCTIONS (CIRCLES)BOOK - ICSECHAPTER - CONSTRUCTIONS (CIRCLES)EXERCISE - EXERCISE
39 Videos
Similar Questions
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
View SolutionIf a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?
View SolutionIn the given figure, ABCDE is a pentagone inscribed in a circle such that AC is a diameter and side BC//AE. If ∠BAC=50∘, find ∠BCE,

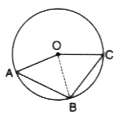
View SolutionIn the given figure, AB is a side of a regular pentagon and BC is the side of a regular hexagon. Find
(i) ∠AOB
(ii) ∠OBC
View SolutionIn a regular pentagon ABCDE, draw a diagonal BE and then find the measure of :
(i) ∠BAE (ii) ∠ABE (iii) ∠BED
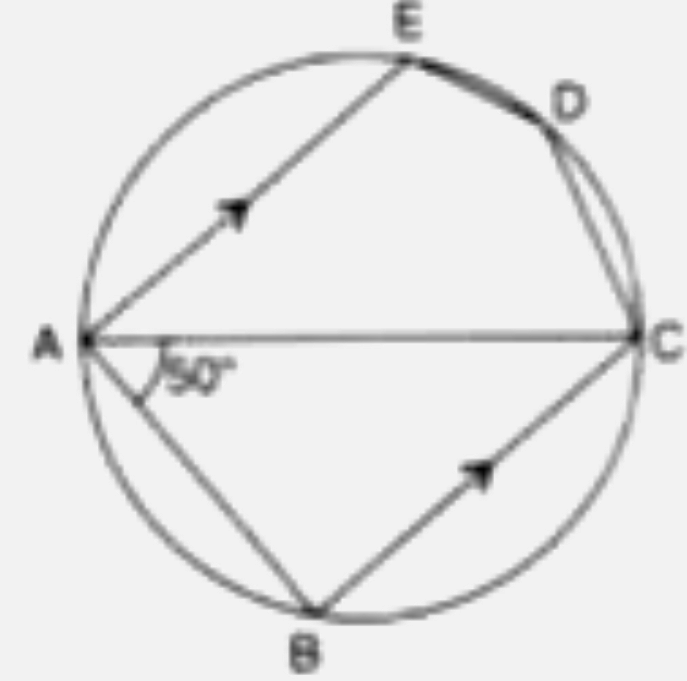
View SolutionIn the given figure, ABCDE is a pentagone inscribed in a circle such that AC is a diameter and side BC//AE. If ∠BAC=50∘, find giving reasons :
(i) ∠ACB
(ii) ∠EDC
(iii) ∠BEC
Hence prove that BE is also a diameter.
View SolutionIf the area of the circle is A1 and the area of the regular pentagon inscribed in the circle is A2, then find the ratio A1A2.
View SolutionIf the area of the circle is A1 and the area of the regular pentagon inscribed in the circle is A2, then find the ratio A1A2.
View SolutionIn a pentagon ABCDE, AB is parallel to ED and angle B=140∘. Find the angles C and D, if ∠C:∠D=5:6
View SolutionA rectangle ABCD is inscribed in a circle. Let PQ be the diameter of the circle parallel the side AB. If ∠BPC=30∘, then the ratio of the area of rectangle to the area of circle is
View Solution
