In a regular pentagon ABCDE, draw a diagonal BE and then find the measure of :
(i) ∠BAE (ii) ∠ABE (iii) ∠BED
The correct Answer is:(i)108∘(ii)36∘(iii)72∘
To solve the problem, we will follow these steps:
Step 1: Calculate the measure of each interior angle of the regular pentagon ABCDE.
The formula for finding the sum of interior angles of a polygon is:
Sum of interior angles=(n−2)×180∘
where n is the number of sides. For a pentagon, n=5.
Sum of interior angles=(5−2)×180∘=3×180∘=540∘
Since it is a regular pentagon, each interior angle is:
Each angle=540∘5=108∘
Step 2: Find the measure of angle BAE.
Since angle BAE is one of the interior angles of the regular pentagon ABCDE, we have:
∠BAE=108∘
Step 3: Analyze triangle ABE.
In triangle ABE, since AB = AE (as sides of the regular pentagon), angles opposite to equal sides are equal. Thus:
∠ABE=∠AEB
Let ∠ABE=∠AEB=x.
Step 4: Use the triangle angle sum property.
The sum of angles in triangle ABE is:
∠BAE+∠ABE+∠AEB=180∘
Substituting the known values:
108∘+x+x=180∘
This simplifies to:
108∘+2x=180∘
2x=180∘−108∘=72∘
x=72∘2=36∘
Thus, we find:
∠ABE=36∘
Step 5: Find the measure of angle BED.
Since angle AED is also an interior angle of the regular pentagon, we have:
∠AED=108∘
Now, we can find angle BED:
∠BED=∠AED−∠ABE=108∘−36∘=72∘
Final Measures:
- ∠BAE=108∘
- ∠ABE=36∘
- ∠BED=72∘
---
Sum of interior angles=(n−2)×180∘
where n is the number of sides. For a pentagon, n=5.
Each angle=540∘5=108∘
∠BAE=108∘
∠ABE=∠AEB
∠BAE+∠ABE+∠AEB=180∘
Substituting the known values:
108∘+x+x=180∘
This simplifies to:
108∘+2x=180∘
2x=180∘−108∘=72∘
x=72∘2=36∘
∠ABE=36∘
∠AED=108∘
∠BED=∠AED−∠ABE=108∘−36∘=72∘
- ∠BAE=108∘
- ∠ABE=36∘
- ∠BED=72∘
Topper's Solved these Questions
- UNDERSTANDING SHAPESBOOK - ICSECHAPTER - UNDERSTANDING SHAPESEXERCISE - Exercise 16C
15 Videos
- UNDERSTANDING SHAPESBOOK - ICSECHAPTER - UNDERSTANDING SHAPESEXERCISE - Exercise 16A
18 Videos
- SURFACE AREA, VOLUME AND CAPACITY. BOOK - ICSECHAPTER - SURFACE AREA, VOLUME AND CAPACITY. EXERCISE - EXERCISE ( E )
11 Videos
Similar Questions
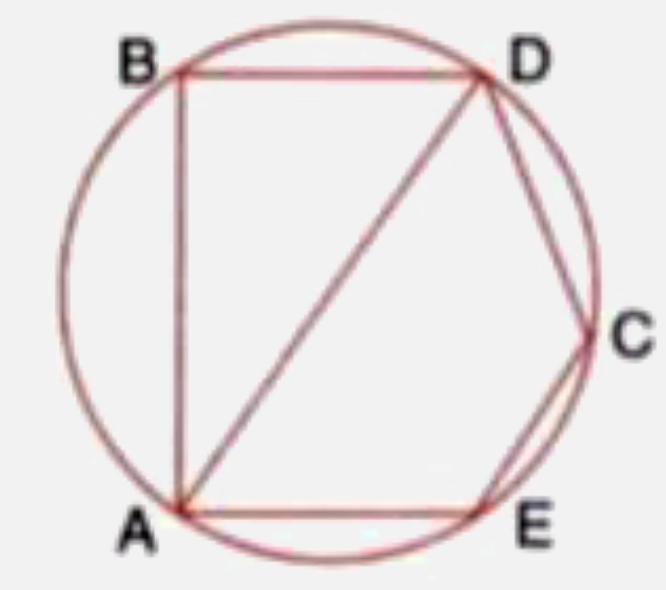
In the given figure , BD is a side of a regular hexagon. DC is a side of a regular pentagon and AD is a diameter , Calculate:
(i) ∠ADC,
(ii) ∠BDA
(iii) ∠ABC
(iv)∠AEC
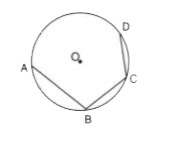
View SolutionIn the given figures , O is the centre of the given circle. AB is a side of a square ,BC
is a side of regular pentagon and CD is a side of regular hexagon. Find:
(i) ∠AOB
(ii) ∠AOC
(iii) ∠AOD
(iv)∠BCD
View Solution
Knowledge Check
Find the measure of the exterior angle of a regular dodecagon.
A15∘B30∘C36∘D144∘
In a regular pentagon ABCDE inscribed in a circle . Find the ratio between angle ADE and angle ADC.
View SolutionFind the radian measure of (i) 25∘ (ii) 240∘.
View Solution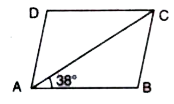
ABCD is a rhombus. If ∠BAC=38∘, find:
(i) ∠ACB
(ii) ∠DAC
(iii) ∠ADC.
View SolutionIn the adjoining figure, ABCD is a square and PAB is an equilateral triangle. Find :
(i) ∠APD
(ii) ∠PDC
(iii) ∠DPC
(iv) Prove that DP=CP

View SolutionIn the given figure, ABCDE is a pentagone inscribed in a circle such that AC is a diameter and side BC//AE. If ∠BAC=50∘, find giving reasons :
(i) ∠ACB
(ii) ∠EDC
(iii) ∠BEC
Hence prove that BE is also a diameter.

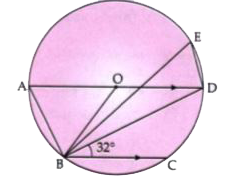
View SolutionIn the figure given below, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD=32∘. Find : (i) ∠OBD (ii) ∠AOB (iii) ∠BED
View SolutionIn a pentagon ABCDE, AB is parallel to ED and angle B=140∘. Find the angles C and D, if ∠C:∠D=5:6
View Solution
