In a triangle PQR, QR = PR and ∠P=36∘. Which is the largest side of the triangle ?
The correct Answer is:PQ
Step by step video, text & image solution for In a triangle PQR, QR = PR and angleP=36^(@). Which is the largest side of the triangle ? by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
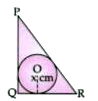
In triangle PQR, PQ = 24 cm, QR = 7 cm and ∠PQR=90∘. Find the radius of the inscribed circle.
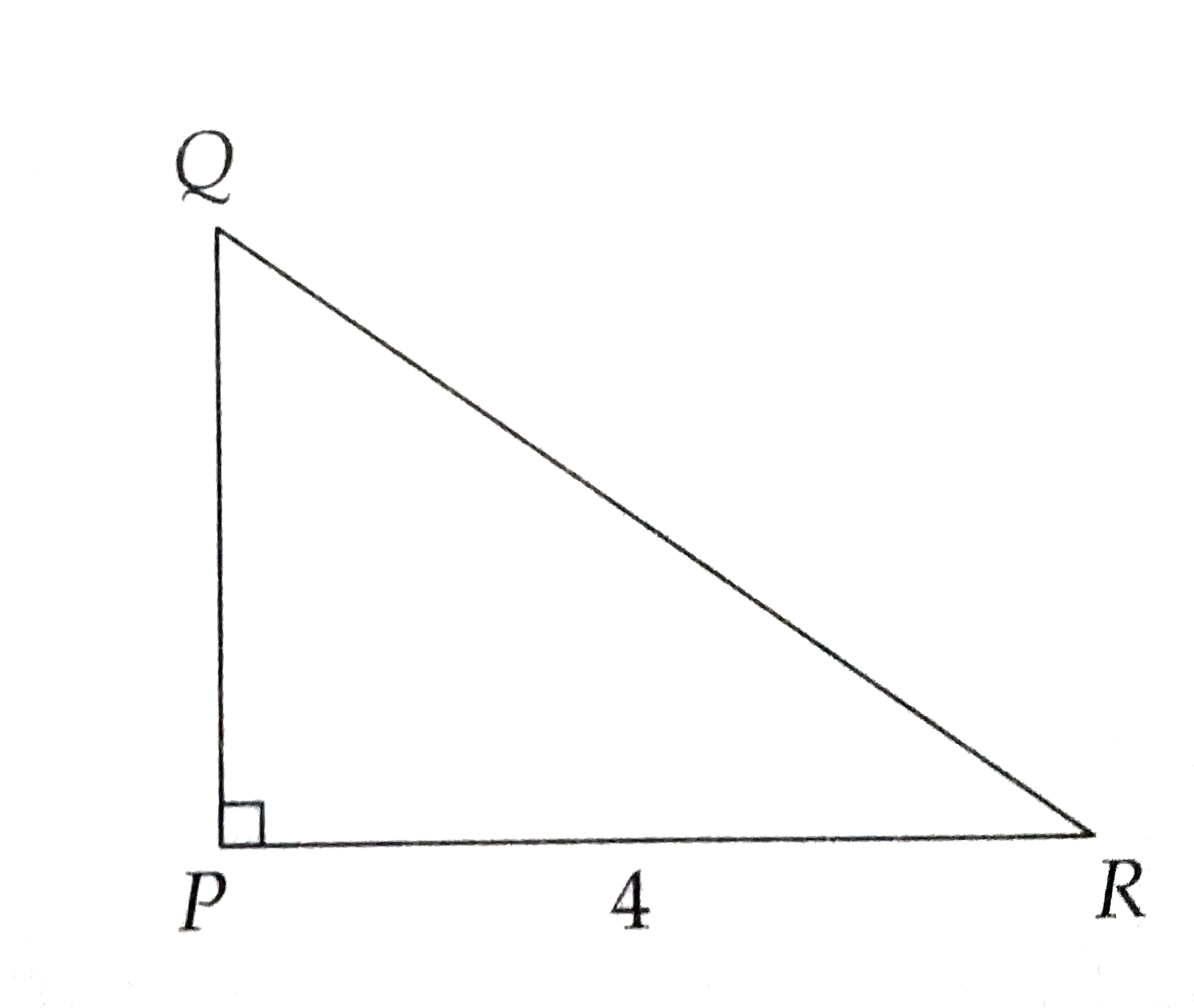
View SolutionIn ΔPQR,∠P=70∘ and ∠R=30∘ .Which side of this triangle is the longest ? Give reason for your answer
View SolutionIn a triangle PQR, P is the largest angle and cosP=13. Further the incircle of the triangle touches the sides PQ, QR and RP at N, L and M respectively, such that the lengths of PN, QL and RM are consecutive even integers. Then possible length(s) of the side(s) of the triangle is (are)
View SolutionA L cm long wire is bent to form a triangle with one of it's angle as 60∘.Find the sides of the triangle for which area is largest.
View SolutionIn a triangle PQR, P is the largest angle and cosP=1/3. Further the incircle of the triangle touches the sides PQ. QR and PR at N, L and M, respectively, such that the length of PN, QL, and RM are consecutive even integers. Then possible length (s) of the side(s) of the triangle is (are)
View SolutionIn a triangle PQR, let ∠PQR=30∘ and the sides PQ and QR have lengths 10√3 and 10, respectively. Then, which of the following statement(s) is (are) TRUE ?
View SolutionConstruct a triangle PQR such that PQ = QR = 4 . 7 cm and ∠Q=72∘ . Measure angles P and R . Name the triangle
View SolutionThe measure of angle angle QPR is 90 degrees, and the area of triangle PQR is 6. If triangle PQR is rotated 360∘ about side PR, what is the total surface area of the resulting solid ?
View SolutionThe sides of a triangle are 16 cm, 12 cm and 20 cm. Find :
(i) area of the triangle
(ii) height of the triangle, corresponding to the largest side
(iii) height of the triangle, corresponding to the smallest side.
View SolutionIn a △ABC, if ∠A=500 and ∠B=600 , determine the shortest and largest sides of the triangle.
View Solution
