In a triangle PQR, P is the largest angle and cosP=1/3. Further the incircle of the triangle touches the sides PQ. QR and PR at N, L and M, respectively, such that the length of PN, QL, and RM are consecutive even integers. Then possible length (s) of the side(s) of the triangle is (are)
16
18
24
22
The correct Answer is:B, D

Let s−a=2k−2,s−b=2k,s−c=2k+2,k∈I,k>1
Adding we get,
s=6k. So, a=4k+2,b=4k,c=4k−2
Now, cosP=13⇒b2+c2−a22bc=13
⇒3[(4k)2+(4k−2)2−(4k+2)2]=2×4k(4k−2)
or 3[16k2−4(4k)×2]=8k(4k−2)
or 48k2−96k=32k2−16kor16k2=80kork=5
So, sides are 22, 20, 18
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Matrix Match Type)
1 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)
3 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (JEE Advanced)
3 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)
1 Videos
Similar Questions
In a triangle PQR, P is the largest angle and cosP=13. Further the incircle of the triangle touches the sides PQ, QR and RP at N, L and M respectively, such that the lengths of PN, QL and RM are consecutive even integers. Then possible length(s) of the side(s) of the triangle is (are)
View SolutionA right triangle has hypotenuse of length p cm and one side of length q cm . If p−q=1 , find the length of the third side of the triangle.
View Solution
Knowledge Check
In triangle PQR. ∠Q is a right angle, QR=24, and PR=26. Triangle YXZ is similar to triangle PQR, where vertices X, Y, and Z correspond to vertices P, Q, and R, respectively, and each side of triangle XYZ is 12 the length of the corresponding side of triangle PQR. What is the value of sin Z?
A513B512C1213D125
ABC is a right triangle, right - angled at the vertex A. A circle is drawn to touch the sides AB and AC at points P and Q respectively such that the other end points of the diameters passing through P and Q lie on the side BC. IF AB = 6 units, then the area (in sq. units) of the circular sector which lies inside the triangle is
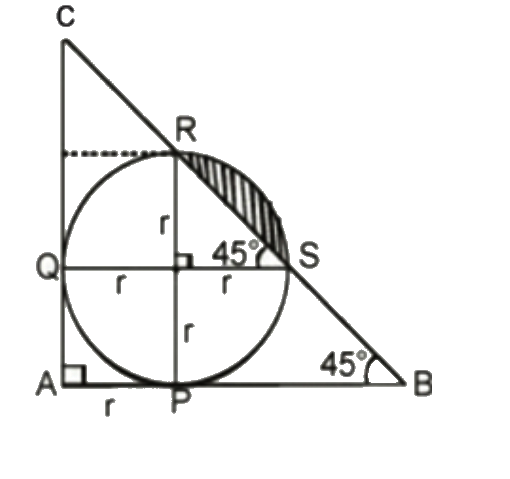
View SolutionIn a triangle PQR, the side QR is extended to S to form the exteiror angle PRS of measure 120∘. If the sides PQ and PR are equal, then prove that the triangle PQR is an equilateral triangle.
View SolutionIf the lengths of the sides of a triangle are 3,5,7, then its largest angle of the triangle is
View SolutionIn a triangle the length of the two larger sides are 24 and 22, respectively.If the angles are in A.P.,then the third side ,is
View SolutionConstruct a triangle PQR, in which PR=6cmandPQ=QR=6.8cm.
Construct the circle which touches QR at R and passes through S.
View SolutionIn a triangle PQR, let ∠PQR=30∘ and the sides PQ and QR have lengths 10√3 and 10, respectively. Then, which of the following statement(s) is (are) TRUE ?
View SolutionWhat is the greatest possible perimeter of a right angled triangle with integer side lengths if one of the sides has length 12?
View Solution
