In the following figure .
(i) if ∠BAD=96∘, find ∠BCDand∠BFE.
(ii) Prove that AD is parallel to PE.
(##SEL_RKB_ICSE_MAT_X_C17_E02_019_Q01.png" width="80%">
(b) ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q . Show that quadrilateral PCDQ is cyclic.
The correct Answer is:each 84∘
Step-by-Step Solution
1. Identify the cyclic quadrilateral:
Since points A, B, C, and D lie on the circumference of a circle, quadrilateral ABCD is a cyclic quadrilateral.
2. Use the property of cyclic quadrilaterals:
In a cyclic quadrilateral, the sum of opposite angles is 180∘. Therefore:
∠BAD+∠BCD=180∘
Substituting the known angle:
96∘+∠BCD=180∘
3. Solve for ∠BCD:
∠BCD=180∘−96∘=84∘
4. Find ∠BFE:
Now consider the angles around point B. Since ∠BCD and ∠BCE form a linear pair:
∠BCD+∠BCE=180∘
Therefore:
84∘+∠BCE=180∘
Solving for ∠BCE:
∠BCE=180∘−84∘=96∘
5. Use the cyclic property again for quadrilateral BCEF:
Since points B, C, E, and F also lie on the circumference of a circle, we have:
∠BCE+∠BFE=180∘
Substituting the known angle:
96∘+∠BFE=180∘
6. Solve for ∠BFE:
∠BFE=180∘−96∘=84∘
Conclusion for part (i):
- ∠BCD=84∘
- ∠BFE=84∘
---
(ii) Prove that AD is parallel to FE:
1. Sum of angles:
We have already calculated:
∠BAD=96∘and∠BFE=84∘
Now, consider the sum of these angles:
∠BAD+∠BFE=96∘+84∘=180∘
2. Conclusion about parallel lines:
Since the sum of the adjacent angles ∠BAD and ∠BFE is 180∘, it follows that lines AD and FE are parallel.
Final Conclusion for part (ii):
- AD∥FE
---
(b) Show that quadrilateral PCDQ is cyclic:
1. Given:
ABCD is a parallelogram, and a circle passes through points A and B, intersecting BC at P and AD at Q.
2. Identify angles:
Since ABCD is a parallelogram, we know:
∠A+∠D=180∘
Let ∠A=θ and ∠D=180∘−θ.
3. Using cyclic properties:
Since points A, B, P, and Q are on the circle, we have:
∠APB+∠AQD=180∘
4. Find opposite angles in quadrilateral PCDQ:
Since ∠PCD+∠QDC are opposite angles in quadrilateral PCDQ, we need to show:
∠PCD+∠QDC=180∘
5. Use the property of opposite angles:
From the properties of the cyclic quadrilateral:
∠PCD+∠QDC=∠A+∠D=180∘
Conclusion for part (b):
- Quadrilateral PCDQ is cyclic.
---
Since points A, B, C, and D lie on the circumference of a circle, quadrilateral ABCD is a cyclic quadrilateral.
In a cyclic quadrilateral, the sum of opposite angles is 180∘. Therefore:
∠BAD+∠BCD=180∘
Substituting the known angle:
96∘+∠BCD=180∘
∠BCD=180∘−96∘=84∘
Now consider the angles around point B. Since ∠BCD and ∠BCE form a linear pair:
∠BCD+∠BCE=180∘
Therefore:
84∘+∠BCE=180∘
Solving for ∠BCE:
∠BCE=180∘−84∘=96∘
Since points B, C, E, and F also lie on the circumference of a circle, we have:
∠BCE+∠BFE=180∘
Substituting the known angle:
96∘+∠BFE=180∘
∠BFE=180∘−96∘=84∘
- ∠BCD=84∘
- ∠BFE=84∘
We have already calculated:
∠BAD=96∘and∠BFE=84∘
Now, consider the sum of these angles:
∠BAD+∠BFE=96∘+84∘=180∘
Since the sum of the adjacent angles ∠BAD and ∠BFE is 180∘, it follows that lines AD and FE are parallel.
- AD∥FE
ABCD is a parallelogram, and a circle passes through points A and B, intersecting BC at P and AD at Q.
Since ABCD is a parallelogram, we know:
∠A+∠D=180∘
Let ∠A=θ and ∠D=180∘−θ.
Since points A, B, P, and Q are on the circle, we have:
∠APB+∠AQD=180∘
Since ∠PCD+∠QDC are opposite angles in quadrilateral PCDQ, we need to show:
∠PCD+∠QDC=180∘
From the properties of the cyclic quadrilateral:
∠PCD+∠QDC=∠A+∠D=180∘
- Quadrilateral PCDQ is cyclic.
Topper's Solved these Questions
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(B)
10 Videos
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )
28 Videos
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )
28 Videos
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (PROBABILITY)
16 Videos
- CONSTRUCTIONS (CIRCLES)BOOK - ICSECHAPTER - CONSTRUCTIONS (CIRCLES)EXERCISE - EXERCISE
39 Videos
Similar Questions
In the given figure ∠BAD=60∘,∠ABD=70∘∠BDC=45∘
(i) prove that AC is a diameter of the circle
(ii) Find ∠ACB
(##SEL_RKB_ICSE_MAT_X_C17_E02_002_Q01.png" width="80%">
View SolutionIn the following figure , angle B=90∘∠ADB=30∘and∠ACB=60∘
If ∠CD=m find AB .
(##SEL_RKB_ICSE_MAT_IX_CR_02_E01_162_Q01.png" width="80%">
View SolutionIn a quadrilateral ABCD, AB = CD and ∠B=∠C. Prove that
AD is parallel to BC.
View SolutionIn the given figure. A is the centre of the circle , ABCD is a parallelogram and CDE is a straight line.
Prove that :∠BCD=2∠ABE
(##SEL_RKB_ICSE_MAT_X_C17_E02_036_Q01.png" width="80%">
View SolutionABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
View SolutionABCD is a parallelogram . The circle passing through the vertices. A, B and C intersects CD (or CD produced) at E. Prove that AE=AD.
View SolutionCalculate the angles x,y and z if
x3=y4=z5
(##SEL_RKB_ICSE_MAT_X_C17_E02_042_Q01.png" width="80%">
View SolutionIn the given figure. AB is the diameter of the circle with centre O.
(##SELRKBICSEMATX_C17E04012_Q01.png width=80%><br>If angle ADC = 32 ^(@) , find angle BOC.
View SolutionIn the following figure AB = AD , AC = AE and ∠BAD=∠CAE,
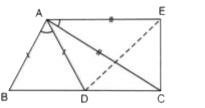
Prove that :BC = ED
View SolutionIn a quadrilateral ABCD, angles A, B, C and D are in the ratio 3:2:1:4 Prove that AD is parallel to BC.
View Solution
