In a circle, with centre O ,a diameter AB and a chord AD are drawn . Another circle is drawn with AO as diameter to cut AD at C. Prove that : BD = 2×OC
The correct Answer is:BD = 2 × OC
To prove that BD=2×OC in the given configuration, we can follow these steps:
Step 1: Identify the triangles
We have two triangles: triangle OAC and triangle BAD.
Step 2: Establish right angles
Since AB is a diameter of the circle, angle BDA is 90∘ (angle in a semicircle). Similarly, since AO is also a diameter of the smaller circle, angle OCA is also 90∘.
Step 3: Identify common angles
In both triangles, angle OAD is common. Therefore, we have:
- ∠BDA=90∘
- ∠OCA=90∘
- ∠OAD=∠BAD
Step 4: Use Angle-Angle (AA) similarity
Since both triangles share a common angle and each has a right angle, by the Angle-Angle (AA) similarity criterion, we can conclude that:
△OAC∼△BAD
Step 5: Set up the proportion of sides
From the similarity of triangles, we can write the following proportions:
BAOA=BDOC
ADAC
Step 6: Substitute the lengths
Let R be the radius of the larger circle. Then:
- BA=2R (diameter of the larger circle)
- OA=R (radius of the smaller circle)
Substituting these values into the proportion gives:
2RR=BDOC
Step 7: Simplify the equation
This simplifies to:
2=BDOC
Step 8: Rearrange to find BD
Multiplying both sides by OC gives:
BD=2×OC
Conclusion
Thus, we have proved that BD=2×OC.
---
We have two triangles: triangle OAC and triangle BAD.
Since AB is a diameter of the circle, angle BDA is 90∘ (angle in a semicircle). Similarly, since AO is also a diameter of the smaller circle, angle OCA is also 90∘.
In both triangles, angle OAD is common. Therefore, we have:
- ∠BDA=90∘
- ∠OCA=90∘
- ∠OAD=∠BAD
Since both triangles share a common angle and each has a right angle, by the Angle-Angle (AA) similarity criterion, we can conclude that:
△OAC∼△BAD
From the similarity of triangles, we can write the following proportions:
BAOA=BDOC
ADAC
Let R be the radius of the larger circle. Then:
- BA=2R (diameter of the larger circle)
- OA=R (radius of the smaller circle)
2RR=BDOC
This simplifies to:
2=BDOC
Multiplying both sides by OC gives:
BD=2×OC
Thus, we have proved that BD=2×OC.
Topper's Solved these Questions
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(A)
58 Videos
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(B)
10 Videos
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (PROBABILITY)
16 Videos
- CONSTRUCTIONS (CIRCLES)BOOK - ICSECHAPTER - CONSTRUCTIONS (CIRCLES)EXERCISE - EXERCISE
39 Videos
Similar Questions
In the given figure, O is the centre of the bigger circle and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10 cm. Find the area of the shaded region

View SolutionProve that the diameter is the greatest chord in a circle.
View SolutionProve that the diameter is the greatest chord in a circle.
View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :
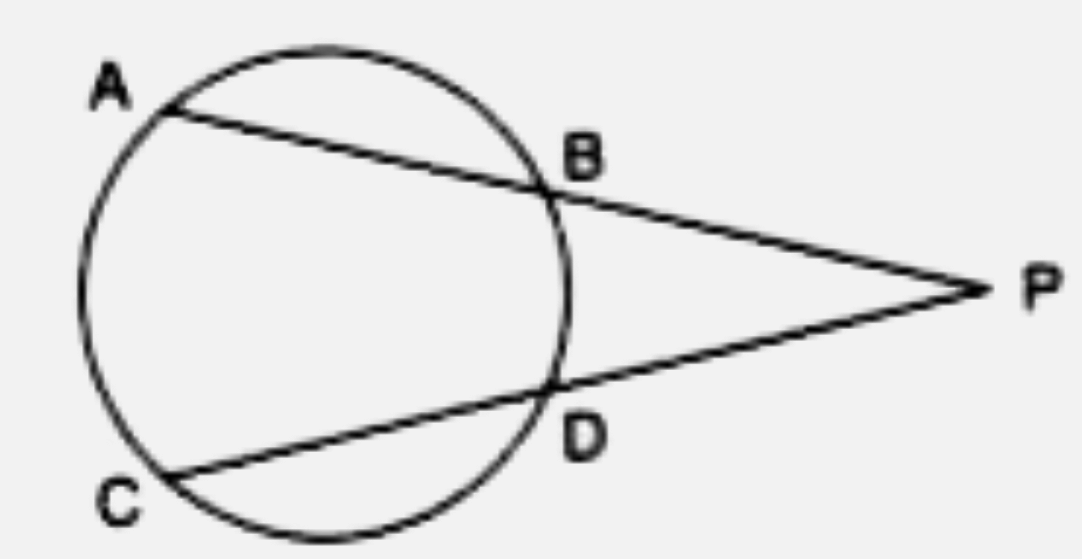
PB=PD
View SolutionBC is an equilateral triangle. A circle is drawn with centre A so that it cuts AB and AC at points M and N respectively. Prove that BN = CM
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
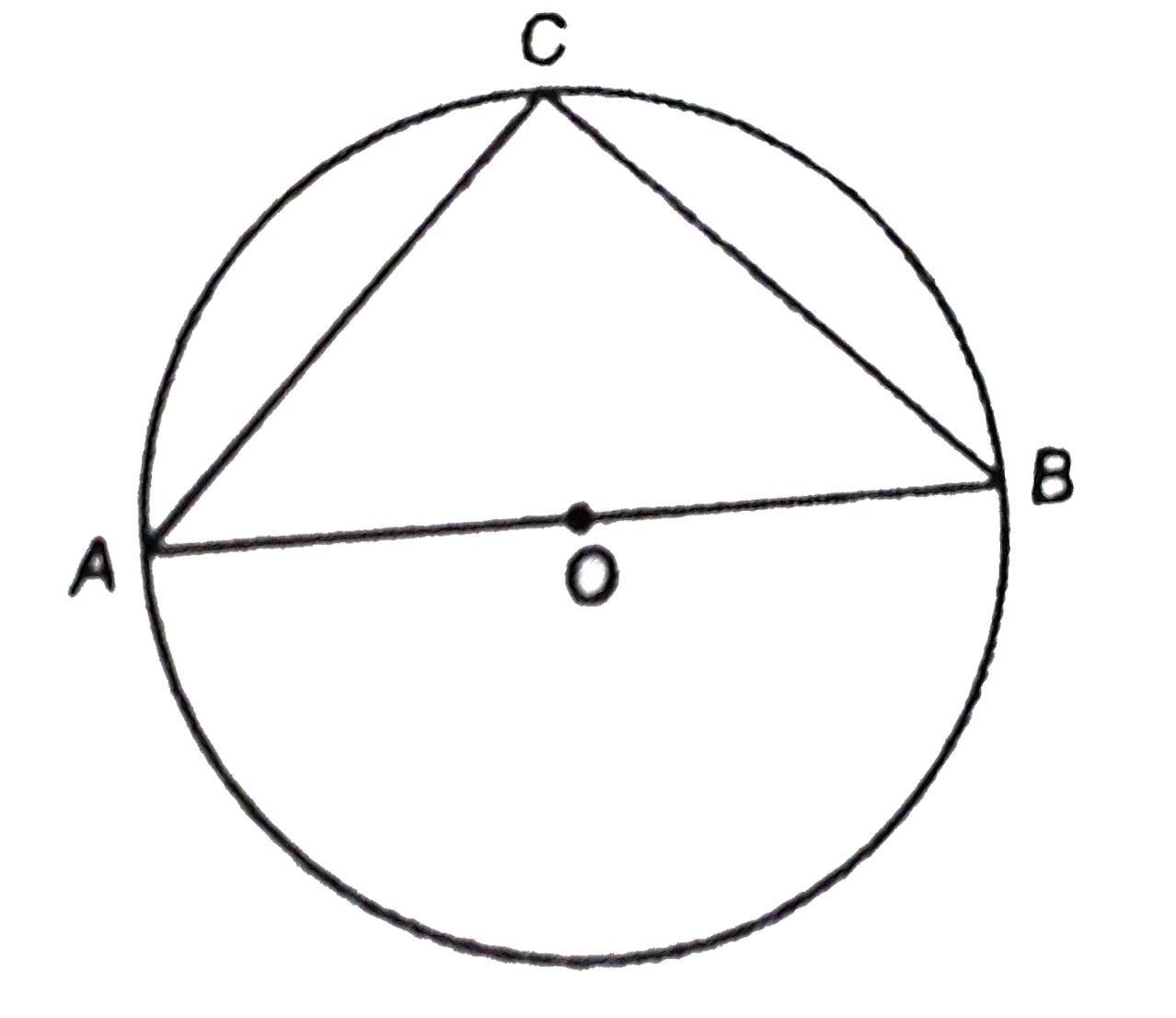
View SolutionO is the centre of a circle of diameter AB. If chord AC= chord BC, then find the value of ∠ABC.
View SolutionThe figure shows two concentric circles and AD is a chord of larger circle.
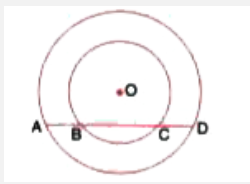
Prove that : AB = CD.
View SolutionTwo tangent segments BC and BD are drawn to a circle with centre O and radius r such that ∠DBC=120∘. Prove that BO=2BC.
View SolutionIn Figure, two tangents ABandAC are drawn to a circle with centre O such that ∠BAC=1200. Prove that OA=2AB
View Solution
