In the adjoining figure PQ = PR and ∠PRQ=70∘ Find ∠QPR.
The correct Answer is:40∘
To solve the problem step by step, we will use the properties of triangles and the information given in the question.
1. Identify the Triangle: We have triangle PQR where PQ = PR and angle PRQ = 70°.
2. Use the Property of Isosceles Triangles: Since PQ = PR, triangle PQR is an isosceles triangle. In an isosceles triangle, the angles opposite the equal sides are equal. Therefore, angle PQR = angle PRQ.
Let ∠PQR=x.
Since PQ = PR, we have:
x=∠PRQ=70°.
3. Calculate the Angles in the Triangle: Now we know that:
∠PQR=70°.
We also denote angle QPR as y.
4. Apply the Angle Sum Property of Triangles: The sum of the angles in a triangle is always 180°. Therefore, we can write:
∠PQR+∠PRQ+∠QPR=180°.
Substituting the known values:
70°+70°+y=180°.
5. Solve for angle QPR:
140°+y=180°.
To find y, subtract 140° from both sides:
y=180°−140°=40°.
6. Conclusion: Therefore, the measure of angle QPR is:
∠QPR=40°.
Final Answer:
∠QPR=40°.
Since PQ = PR, we have:
x=∠PRQ=70°.
∠PQR=70°.
We also denote angle QPR as y.
∠PQR+∠PRQ+∠QPR=180°.
Substituting the known values:
70°+70°+y=180°.
140°+y=180°.
To find y, subtract 140° from both sides:
y=180°−140°=40°.
∠QPR=40°.
∠QPR=40°.
Topper's Solved these Questions
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(A)
58 Videos
- CIRCLESBOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(B)
10 Videos
- CHAPTERWISE REVISION EXERCISEBOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (PROBABILITY)
16 Videos
- CONSTRUCTIONS (CIRCLES)BOOK - ICSECHAPTER - CONSTRUCTIONS (CIRCLES)EXERCISE - EXERCISE
39 Videos
Similar Questions
In the adjoining figure ∠QPO=24∘ and ∠SPR=20∘ , find the value of ∠QOR.

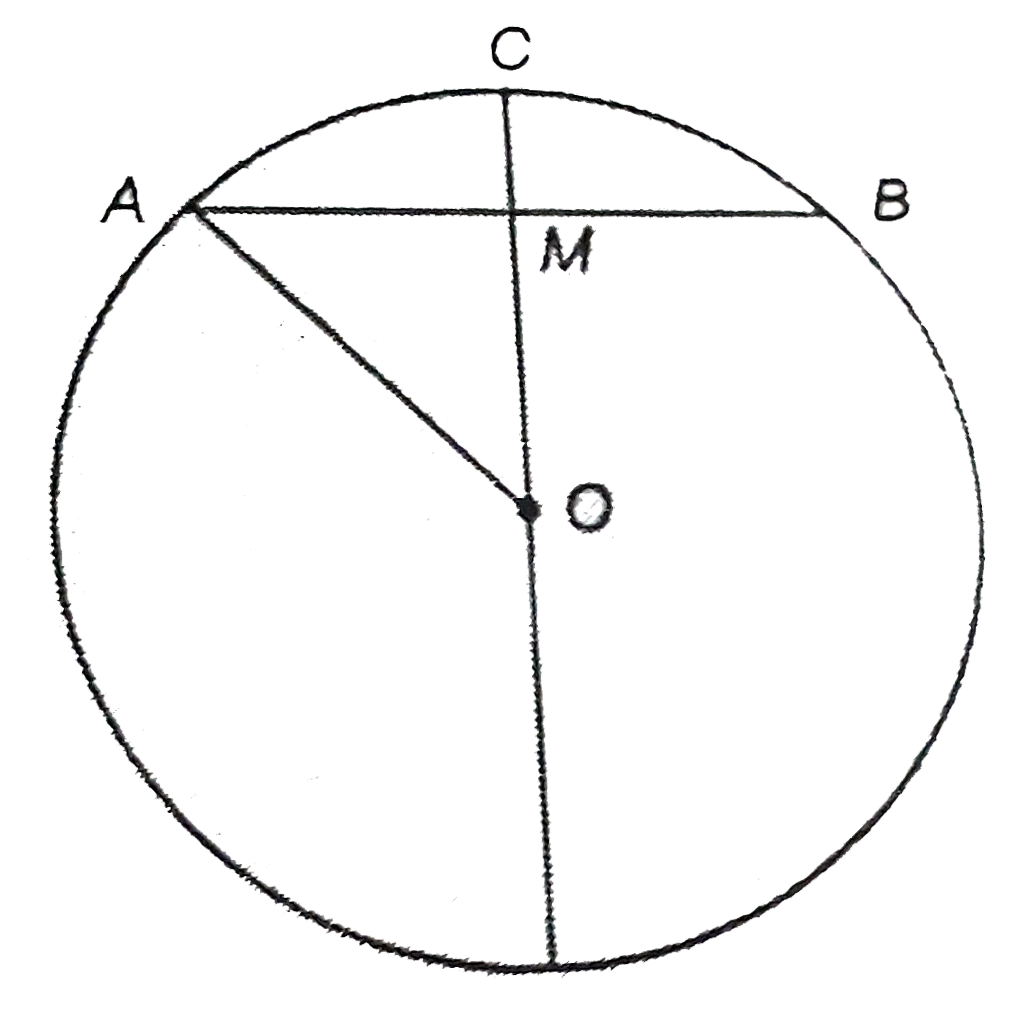
View SolutionIn the adjoining figure, AP=8cm, BP=2cm and ∠CPA=90∘. Find the length of chord CD.
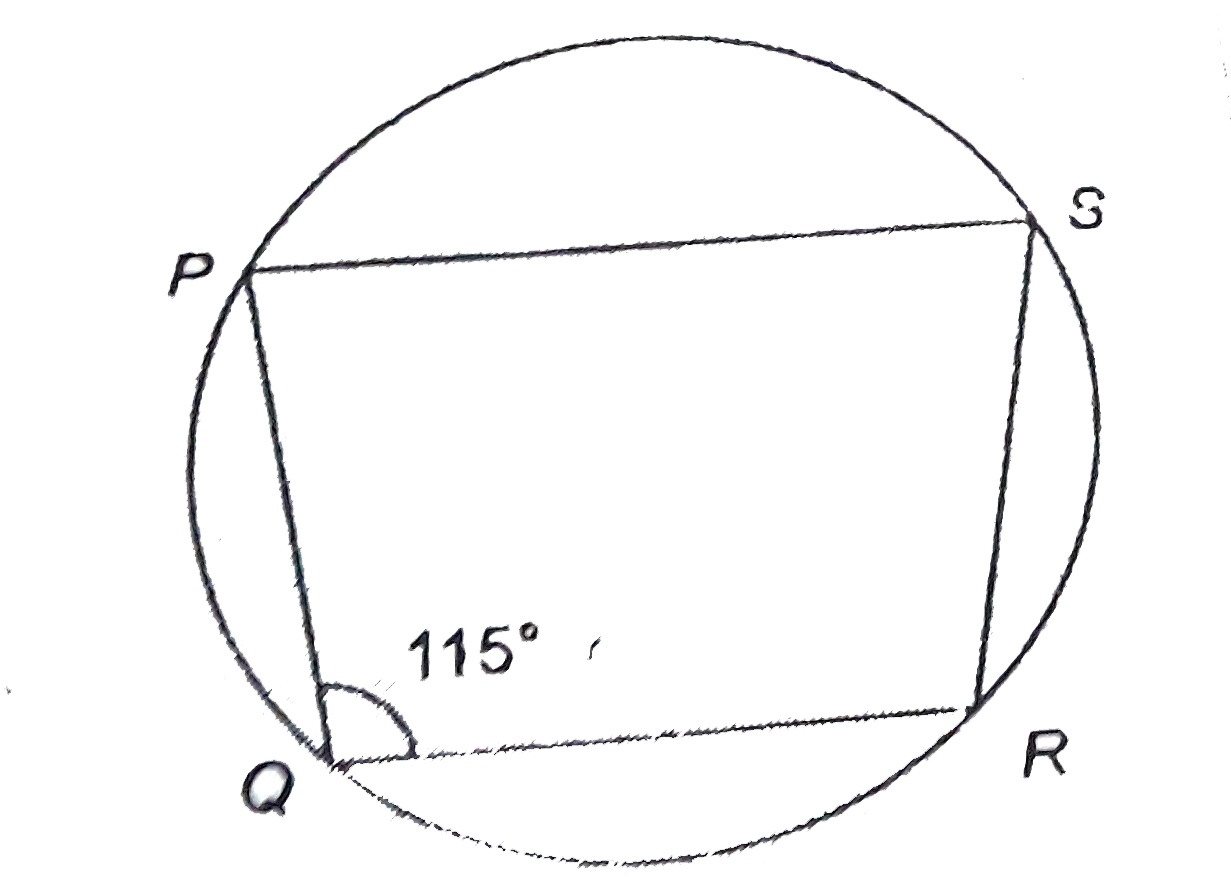
View SolutionIn the adjoining figure, PS| |QR and ∠Q=115∘, then find the values of ∠P, anl≥R and ∠S.
View SolutionIn the adjoining figure , ∠AOC=110∘, Calculate :
∠OAC
View SolutionIn the adjoining figure , ∠AOC=110∘, Calculate :
∠ADC
View SolutionIn the adjoining figure , ∠AOC=110∘, Calculate :
∠ABC
View SolutionIn the adjoining figure, find AC . (FIGURE)
View SolutionIn the adjoining figure, if ∠ACB=40∘, ∠DPB=120∘, then find ∠CBD.

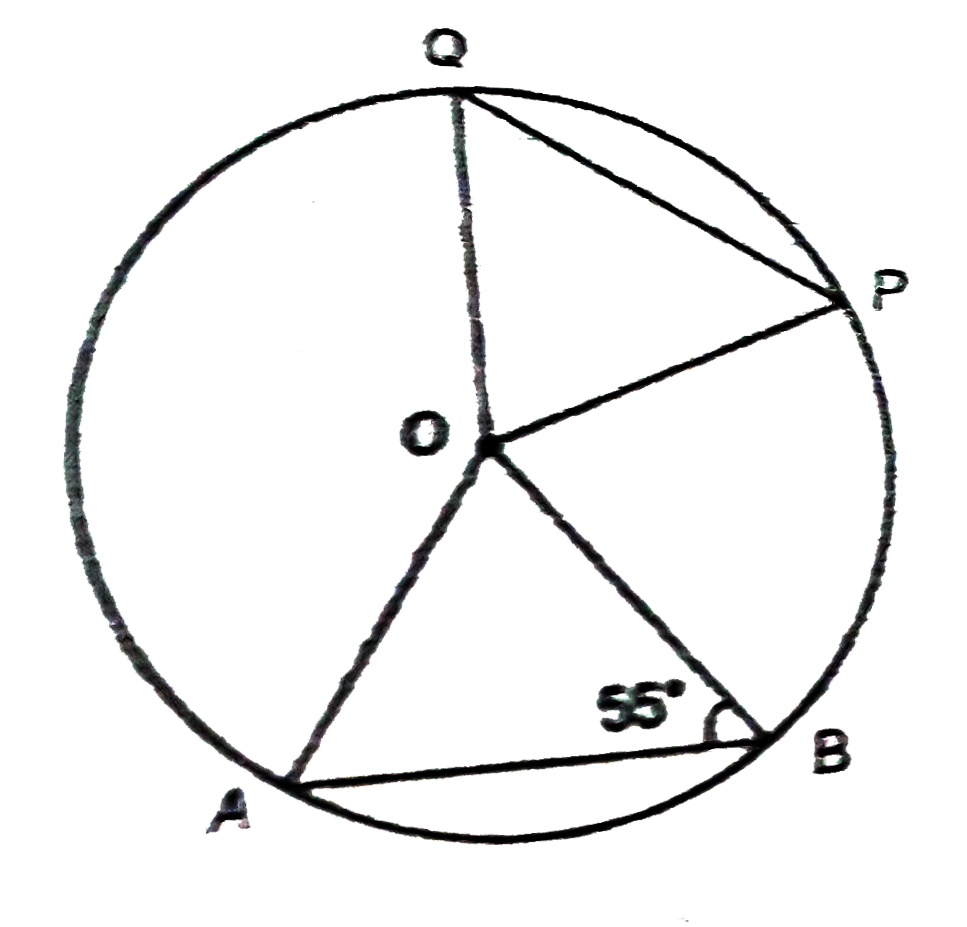
View SolutionIn the adjoining figure, chord AB= chord PQ. If ∠OBA=55∘, then find ∠POQ.
View SolutionIn the adjoining figure, ∠ABC=95∘ and ∠DAC=35∘, then find the value of ∠ACD.

View Solution
