When a piece of wood is suspended from the hook of a spring balance, it reads 70 gf. The wood is now lowered into water.What reading do you expect on the scale of spring balance?
The correct Answer is:zero
To solve the problem, we need to understand the concept of buoyancy and Archimedes' principle. When an object is submerged in a fluid, it experiences an upward force called buoyant force, which reduces the effective weight of the object in the fluid.
1. Identify the Weight of the Wood in Air:
The wood weighs 70 gf (gram-force) when suspended in air. This is the force due to gravity acting on the wood.
2. Understand the Concept of Buoyant Force:
When the wood is submerged in water, it will experience an upward buoyant force. According to Archimedes' principle, the buoyant force is equal to the weight of the fluid displaced by the submerged part of the object.
3. Determine the Buoyant Force:
The buoyant force acting on the wood will reduce the effective weight of the wood when it is submerged in water. The amount of buoyant force depends on the volume of the wood and the density of water.
4. Calculate the New Reading on the Spring Balance:
Since the wood is floating, the reading on the spring balance will be equal to the weight of the wood minus the buoyant force. However, since we do not have the specific volume or density of the wood, we can conclude that the reading will be less than 70 gf.
5. Conclusion:
The reading on the spring balance when the wood is submerged in water will be less than 70 gf. The exact value cannot be determined without additional information about the wood's volume and density.
Expected Reading:
The reading on the spring balance when the wood is submerged in water will be less than 70 gf.
The wood weighs 70 gf (gram-force) when suspended in air. This is the force due to gravity acting on the wood.
When the wood is submerged in water, it will experience an upward buoyant force. According to Archimedes' principle, the buoyant force is equal to the weight of the fluid displaced by the submerged part of the object.
The buoyant force acting on the wood will reduce the effective weight of the wood when it is submerged in water. The amount of buoyant force depends on the volume of the wood and the density of water.
Since the wood is floating, the reading on the spring balance will be equal to the weight of the wood minus the buoyant force. However, since we do not have the specific volume or density of the wood, we can conclude that the reading will be less than 70 gf.
The reading on the spring balance when the wood is submerged in water will be less than 70 gf. The exact value cannot be determined without additional information about the wood's volume and density.
The reading on the spring balance when the wood is submerged in water will be less than 70 gf.
Topper's Solved these Questions
- UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATIONBOOK - ICSECHAPTER - UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATIONEXERCISE - EXERCISE 5(c) (Multiple Choice Question)
3 Videos
- UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATIONBOOK - ICSECHAPTER - UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATIONEXERCISE - EXERCISE 5(c) (Numerical)
9 Videos
- UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATIONBOOK - ICSECHAPTER - UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATIONEXERCISE - EXERCISE 5(B) (Numerical)
16 Videos
- SOUNDBOOK - ICSECHAPTER - SOUNDEXERCISE - TOPIC 2 Infrasonic and Ultrasonic Waves ( 3 Marks Questions)
3 Videos
Similar Questions
a metal solid cylinder tied ot a thread is hanging from the hook of a spring balance. The cylinder is gradually immersed into water contaned in a jar. What changes do you expect in the readings of spring balance? Explain your answer.
View SolutionThe reading in the spring balance is

View SolutionThe reading in the spring balance is:

View SolutionA cubical block (side l) is in equilibrium at the interface of two liquids A and B. The spring balance reads W Newton. If the block is weighted in air, the reading of the spring balance will be :

View SolutionAn object is suspended from a spring balance in a lift. The reading is 240 N when the lift is at rest. If the spring balance reading now change to 220N, then the lift is moving
View SolutionA wooden block of volume 1000cm3 is suspended from a spring balance its weight is 12 N in air. It is suspended in water such that half of the block is below the surface of water. The reading of spring balance is
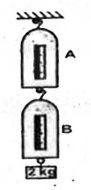
View SolutionA block of mass 2kg is suspended through two light spring balances A and B. Then A and B will read respectively
View SolutionA 20N metal block is suspended by a spring balance. A beaker containing some water is placed on a weighing machine which reads 40N. The spring balance is now lowered so that the block gets immersed in the water. The spring balance now reads 16N. The reading of the weighing machine will be.
View SolutionFor the arrangement shown in the figure, the reading of spring balance is

View SolutionA block of mass 4 kg and volume 5×10−4m3 is suspended by a spring balance in a lift which is accelerating. The apparent weight shown by the spring balance is 3 kg. Now the block is immersed in water in kg shown by the spring balance is
View Solution
