When a tree is cut, the cutter makes a cut on the side facing the direction in which he wants it to fall. Why ? Explain.
To understand why a cutter makes a cut on the side of the tree facing the direction in which he wants it to fall, we can break down the explanation into several steps:
1. Understanding Torque:
- Torque is a measure of the rotational force acting on an object. In the case of a tree, when it is standing upright, its weight (mg) acts downwards at its center of mass.
2. Point of Cut:
- When the cutter makes a cut on one side of the tree, this cut creates a point of rotation. The tree will rotate around this point when it begins to fall.
3. Direction of Cut:
- If the cut is made on the side facing the direction in which the cutter wants the tree to fall, the weight of the tree will create a torque that causes it to rotate in that desired direction.
4. Torque Calculation:
- The torque (τ) produced by the weight of the tree can be calculated as τ = r × F, where r is the distance from the point of cut (pivot point) to the center of mass of the tree, and F is the force due to gravity (mg). When the cut is made on the side facing the desired direction, the distance r is maximized, thus maximizing the torque.
5. Resulting Motion:
- As the torque acts on the tree, it will begin to rotate about the cut point and fall in the intended direction. If the cut were made on the opposite side, the torque would not effectively cause the tree to fall in the desired direction.
Conclusion:
The cutter makes a cut on the side facing the direction he wants the tree to fall because this allows the weight of the tree to create a torque that facilitates the fall in that direction.
- Torque is a measure of the rotational force acting on an object. In the case of a tree, when it is standing upright, its weight (mg) acts downwards at its center of mass.
- When the cutter makes a cut on one side of the tree, this cut creates a point of rotation. The tree will rotate around this point when it begins to fall.
- If the cut is made on the side facing the direction in which the cutter wants the tree to fall, the weight of the tree will create a torque that causes it to rotate in that desired direction.
- The torque (τ) produced by the weight of the tree can be calculated as τ = r × F, where r is the distance from the point of cut (pivot point) to the center of mass of the tree, and F is the force due to gravity (mg). When the cut is made on the side facing the desired direction, the distance r is maximized, thus maximizing the torque.
- As the torque acts on the tree, it will begin to rotate about the cut point and fall in the intended direction. If the cut were made on the opposite side, the torque would not effectively cause the tree to fall in the desired direction.
The cutter makes a cut on the side facing the direction he wants the tree to fall because this allows the weight of the tree to create a torque that facilitates the fall in that direction.
Topper's Solved these Questions
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM EQUATIONS OF ROTATIONAL MOTION)
Explore 8 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM CENTRE OF MASS)
Explore 8 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (SHORT ANSWER QUESTIONS)
Explore 35 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
Explore 50 Videos
Similar Questions
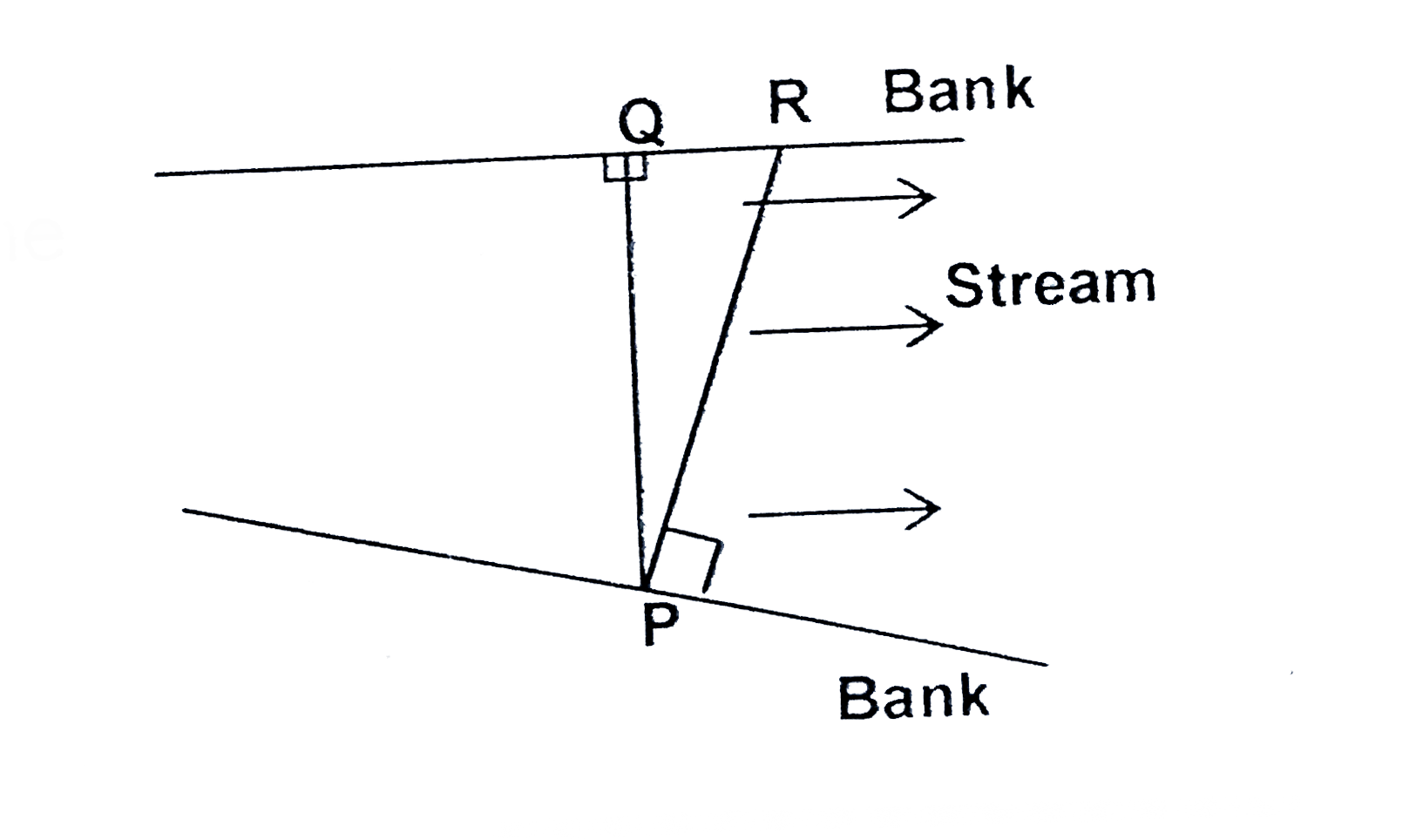
In a lake, stream direction is as shown in the figure. A man starting from the point P on the bank wants to move to the otherside of the bank in shortest time .Then direction in which he should swim
View SolutionFind the equation of the straight line which makes an angle of 15∘ with the positive direction of x-axis and which cuts and intercept of length 4 on then negative direction of y-axis.
View SolutionA swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as shown. The velocity of the swimmer in still water is same as that of the water
(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity ? Calculate angle between his velocity and river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.

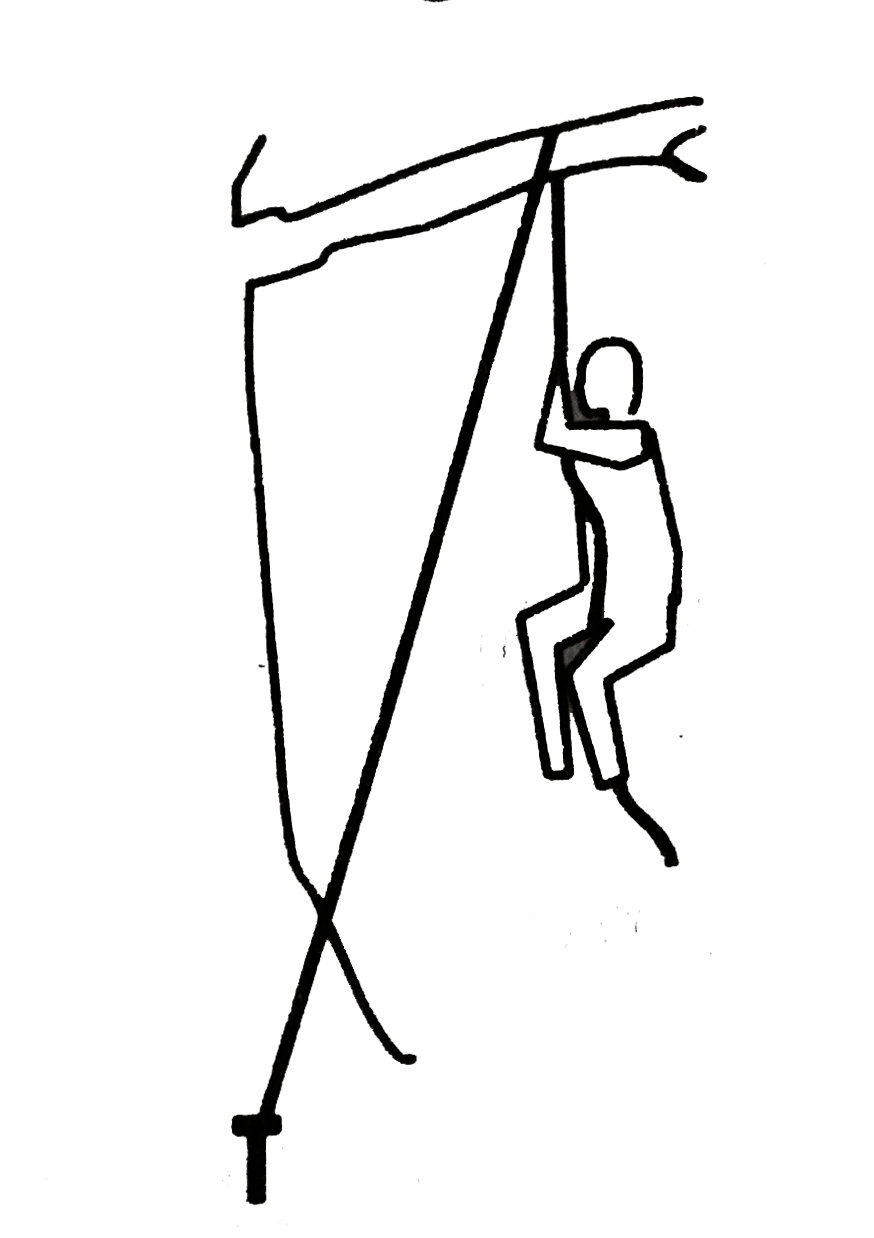
View SolutionA light rope fixed at one end of a wooden clamp on the ground passes over a tree branch and hangs on the other side. It makes an angle of 300 with the ground. A man weighing (60 kg) wants to climb up the rope. The wooden clamp can come out of the ground if an upward force greater than 360 N is applied it. Find the maximum acceleration in the upward direction with which the man can climb safely. Neglect friction at the tree branch. Take g=10ms2
View SolutionFind the equation of the circle which is touched by y=x , has its center on the positive direction of the x=axis and cuts off a chord of length 2 units along the line √3y−x=0
View SolutionFind the equation of the circle which is touched by y=x , has its center on the positive direction of the x=axis and cuts off a chord of length 2 units along the line √3y−x=0
View SolutionFind the equation of the line which cuts off an intercept 4 on the positive direction of x-axis and an intercept 3 on the negative direction of y-axis.
View SolutionThe base of an isosceles triangle measures 4 units base angle is equal to 45∘. A straight line cuts the extension of the base at a point M at the angle θ and bisects the lateral side of the triangle which is nearest to M.
The area of quadrilateral which the straight line cuts off from the given triangle is
View SolutionThe base of an isosceles triangle measures 4 units base angle is equal to 45∘. A straight line cuts the extension of the base at a point M at the angle θ and bisects the lateral side of the triangle which is nearest to M.
The possible range of values in which area of quadrilateral which straight line cuts off from the given triangle lie in (a) (5/2, 7/2) (b) (4,3) (c) (4,5) (d) (3,4)
View SolutionA rectangular cardboard sheet has length 32 cm and breadth 26 cm. The four squares each of side 3 cm are cut from the corners of the sheet and the sides are folded to make a rectanguler container. Find the capacity of the container.
View Solution