Show that the torque acting on a body is equal to the product of moment of inertia and the angular acceleration of the body.
To show that the torque acting on a body is equal to the product of moment of inertia and the angular acceleration of the body, we can follow these steps:
Step 1: Define Torque
Torque (τ) is defined as the product of the radius vector (r) and the force (F) applied at that radius, mathematically expressed as:
τ=r×F
Step 2: Relate Force to Mass and Acceleration
According to Newton's second law, the force acting on an object is the product of its mass and acceleration. For rotational motion, we can express the linear acceleration (a) in terms of angular acceleration (α):
F=m⋅a
For a point mass at a distance r from the axis of rotation, the linear acceleration is given by:
a=r⋅α
Thus, we can substitute this into the force equation:
F=m⋅(r⋅α)=mrα
Step 3: Substitute Force into Torque Equation
Now, substituting the expression for force into the torque equation, we have:
τ=r×(mrα)
Since torque is a scalar quantity in this context, we can simplify this to:
τ=mr2α
Step 4: Consider Multiple Masses
If we have multiple point masses m1,m2,…,mn located at distances r1,r2,…,rn from the axis of rotation, the total torque will be the sum of the individual torques:
τtotal=τ1+τ2+…+τn=(m1r21α)+(m2r22α)+…+(mnr2nα)
Step 5: Factor Out Angular Acceleration
Factoring out the common term α:
τtotal=α(m1r21+m2r22+…+mnr2n)
Step 6: Define Moment of Inertia
The moment of inertia (I) is defined as:
I=m1r21+m2r22+…+mnr2n
Thus, we can rewrite the total torque as:
τtotal=I⋅α
Conclusion
We have shown that the torque acting on a body is equal to the product of its moment of inertia and its angular acceleration:
τ=I⋅α
Torque (τ) is defined as the product of the radius vector (r) and the force (F) applied at that radius, mathematically expressed as:
τ=r×F
According to Newton's second law, the force acting on an object is the product of its mass and acceleration. For rotational motion, we can express the linear acceleration (a) in terms of angular acceleration (α):
F=m⋅a
For a point mass at a distance r from the axis of rotation, the linear acceleration is given by:
a=r⋅α
Thus, we can substitute this into the force equation:
F=m⋅(r⋅α)=mrα
Now, substituting the expression for force into the torque equation, we have:
τ=r×(mrα)
Since torque is a scalar quantity in this context, we can simplify this to:
τ=mr2α
If we have multiple point masses m1,m2,…,mn located at distances r1,r2,…,rn from the axis of rotation, the total torque will be the sum of the individual torques:
τtotal=τ1+τ2+…+τn=(m1r21α)+(m2r22α)+…+(mnr2nα)
Factoring out the common term α:
τtotal=α(m1r21+m2r22+…+mnr2n)
The moment of inertia (I) is defined as:
I=m1r21+m2r22+…+mnr2n
Thus, we can rewrite the total torque as:
τtotal=I⋅α
We have shown that the torque acting on a body is equal to the product of its moment of inertia and its angular acceleration:
τ=I⋅α
Topper's Solved these Questions
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (VERY SHORT ANSWER QUESTIONS)
Explore 14 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (FROM EQUATIONS OF ROTATIONAL MOTION)
Explore 8 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (LONG ANSWER QUESTIONS)
Explore 14 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
Explore 50 Videos
Similar Questions
Knowledge Check
The torque acting on a body is the rotational, analogue of
Amass of the bodyBlinear kinetic energy of the bodyClinear velocity of the bodyDforce in linear motion
If the torque on a body is zero, then?
View SolutionCompute the torque acting on a wheel of moment of inertia 10kgm2, moving with angular acceleration 5rads−2.
View SolutionCompute the torque acting on a wheel of moment of inertia 10kgm2, moving with angular acceleration 5rads−2.
View SolutionDefine torque. Show that it is equal to the product of force and lever arm.
View SolutionIf a constant torque acts on a body, the body?
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
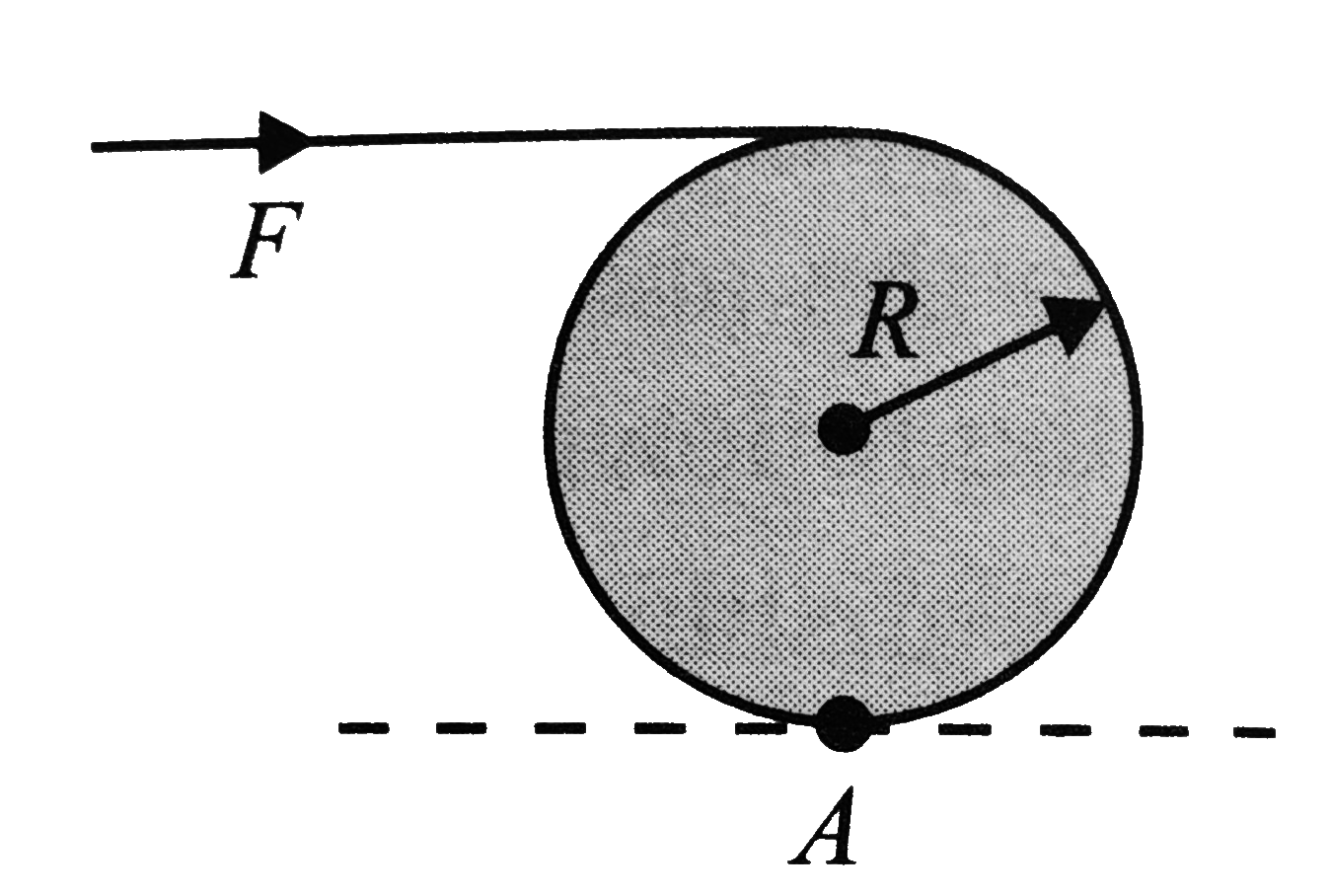
Tangential acceleration of the centre of mass is
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
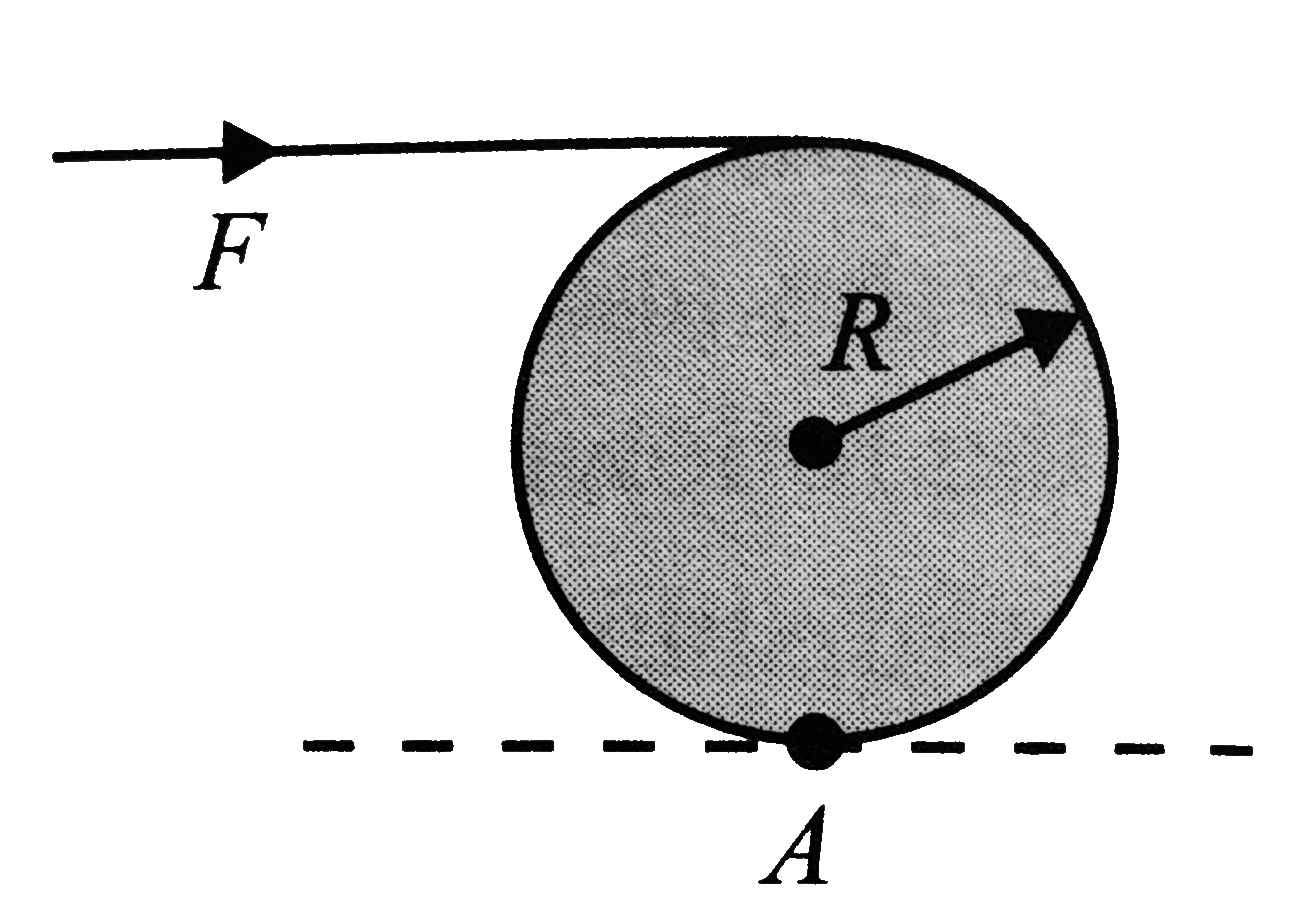
Component of reaction at the hinge in the horizontal direction is
View Solution

