How is the swimmer jumping into water from a height be able to make loop in air ?
To understand how a swimmer jumping into water from a height can make a loop in the air, we can analyze the situation using the principles of angular momentum. Here’s a step-by-step explanation:
Step 1: Understanding Angular Momentum
Angular momentum (L) is defined as the product of the moment of inertia (I) and the angular velocity (ω) of an object. The formula is given by:
L=I⋅ω
Step 2: Conservation of Angular Momentum
According to the law of conservation of angular momentum, if no external torque acts on a system, the total angular momentum of that system remains constant. This means:
Linitial=Lfinal
or
I1⋅ω1=I2⋅ω2
where I1 and ω1 are the initial moment of inertia and angular velocity, and I2 and ω2 are the final moment of inertia and angular velocity.
Step 3: Moment of Inertia
The moment of inertia depends on how mass is distributed relative to the axis of rotation. When the swimmer jumps and extends their arms and legs, their moment of inertia is larger. Conversely, when they pull their arms and legs inward, their moment of inertia decreases.
Step 4: Effect of Pulling Limbs Inward
When the swimmer pulls their arms and legs inward:
- The moment of inertia (I) decreases.
- According to the conservation of angular momentum, if I decreases, then ω (angular velocity) must increase to keep the angular momentum constant.
Step 5: Making a Loop
As the swimmer pulls their limbs inward, the increase in angular velocity allows them to rotate faster. This increased rotational speed helps them to complete a loop in the air before entering the water.
Conclusion
Thus, by manipulating their body position and using the conservation of angular momentum, the swimmer can successfully perform a loop in the air while jumping from a height.
---
Angular momentum (L) is defined as the product of the moment of inertia (I) and the angular velocity (ω) of an object. The formula is given by:
L=I⋅ω
According to the law of conservation of angular momentum, if no external torque acts on a system, the total angular momentum of that system remains constant. This means:
Linitial=Lfinal
or
I1⋅ω1=I2⋅ω2
where I1 and ω1 are the initial moment of inertia and angular velocity, and I2 and ω2 are the final moment of inertia and angular velocity.
The moment of inertia depends on how mass is distributed relative to the axis of rotation. When the swimmer jumps and extends their arms and legs, their moment of inertia is larger. Conversely, when they pull their arms and legs inward, their moment of inertia decreases.
When the swimmer pulls their arms and legs inward:
- The moment of inertia (I) decreases.
- According to the conservation of angular momentum, if I decreases, then ω (angular velocity) must increase to keep the angular momentum constant.
As the swimmer pulls their limbs inward, the increase in angular velocity allows them to rotate faster. This increased rotational speed helps them to complete a loop in the air before entering the water.
Thus, by manipulating their body position and using the conservation of angular momentum, the swimmer can successfully perform a loop in the air while jumping from a height.
Topper's Solved these Questions
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (LONG ANSWER QUESTIONS)
14 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (SHORT ANSWER QUESTIONS)
35 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (FROM BANKING OR RAILS AND ROADS)
13 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
Similar Questions
Velamen found in epiphytic roots is meant for
(a) absorption of water from host
(b) absorption of water from air
(c) perennation
(d) protection
View SolutionAssertion : When we jump from height then maximum possibilities to get hurt is at foot.
Reason : Maximum force is exerted on foot.
View SolutionWhen light enters from air to water, then its
View SolutionThe string AB vibrates in two loops with a tuning fork when block hasngs in air. Now block is completely immersed in water, the string vibrates in three loops with same tuning fork. The specific gravity of block is :

View SolutionHow is water drawn up from a well by a water pump ?
View SolutionThe main function of loop of henle is the reabsorption of water from the contents of renal tubules. In which of the following will the loop of Henle be poorly developed or even absent?
View SolutionThe speed of a swimmer in still water is 20 m//s. The speed of river water of river water is 10 m//s and due east. If he is standing on the south bank and wishes to cross the river along the shortest path the angle at which he should make his stroke w.r.t. noth is given by :-
View SolutionWhen air of density 1.3kg/m3 flows across the top of the tube shown in the accompanying figure, water rises in the tube to a height of 1.0cm. What is the speed of air?

View Solution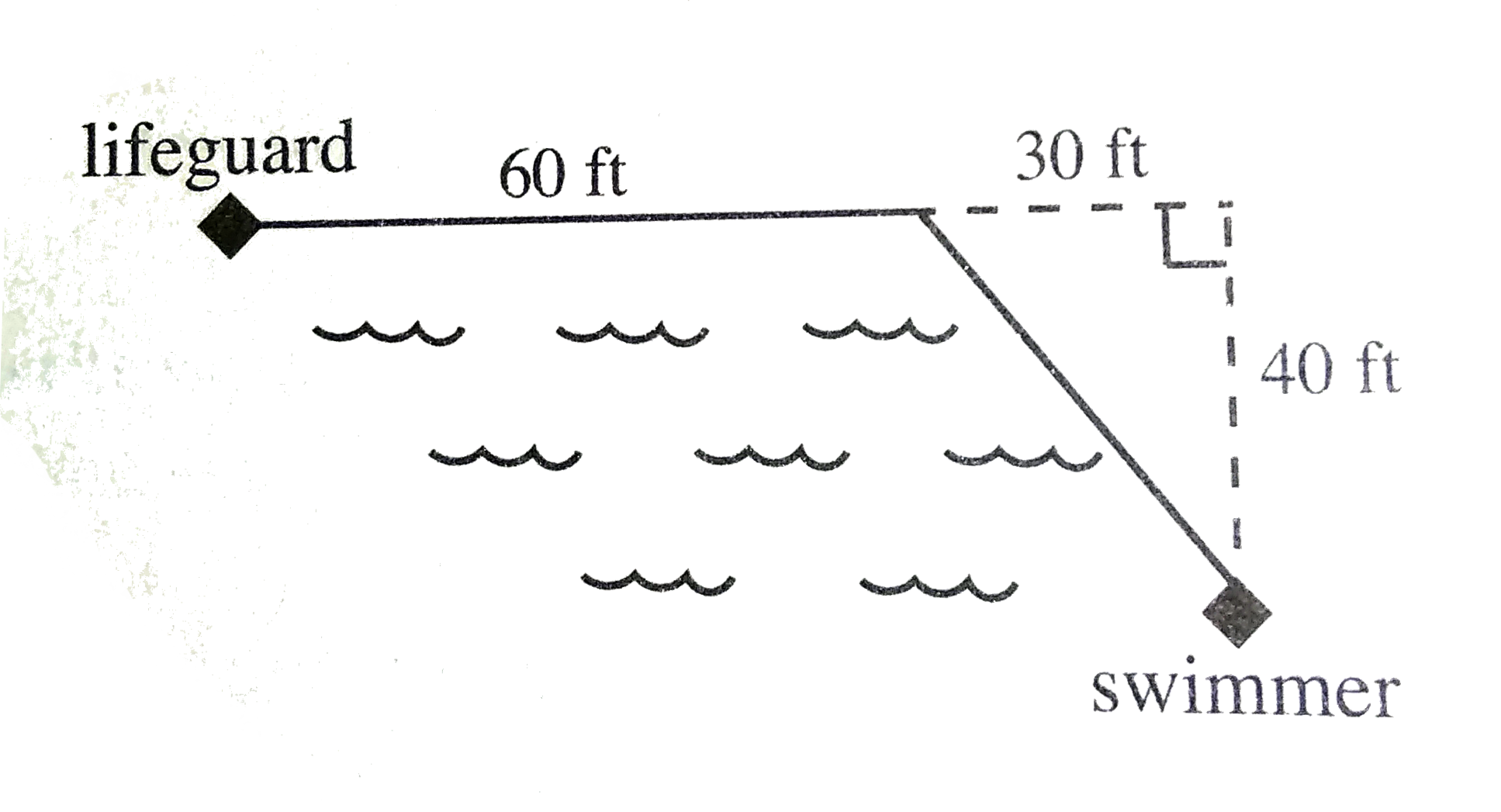
As shown in the figure above, a lifeguard sees a struggling swimmer who is 40 feet from the beach. The lifeguard runs 60 feets along the edge of the water at a speed of 12 feet per second. He pauses for 1 seconds to locate the swimmer again, and then dives into the water and swims along a diagonal path to the swimmer at a speed of 5 feet per second. How many seconds go by between the time the lifeguard sees the struggling swimmer and the times he reaches the swimmer?
View SolutionAn expansible balloon filled with air is floating on the top surface of a lake, with 2/3 of its volume is submerged in water. How deep should it be sunk in water without changing the temperature of air in it, in order that it is just in equilibrium, neither sinking nor rising further? Height of water barometer =10m.
View Solution
