Question

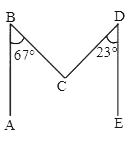
In a triangle ABC, $\angle B=\angle C={78}^{\circ }$. D & E are two points on side AB and AC such that $\angle BCD={51}^{\circ }\text{and}\angle CBE={24}^{\circ }$. Find angle $\angle CDE=$?

Answer

`12^(@)`

Explanation

To find the angle $$\angle CDE$$ in triangle $$ABC$$ with the given angles, we can follow these steps:

1. Identify Given Angles:
- \( \angle B = \angle C = 78^\circ \)
- \( \angle BCD = 51^\circ \)
- \( \angle CBE = 24^\circ \)

2. Calculate Angle \( A \):
- In triangle \( ABC \), the sum of angles is \( 180^\circ \).
\( \angle A = 180^\circ - \angle B - \angle C = 180^\circ - 78^\circ - 78^\circ = 24^\circ \)

3. Calculate Angle \( BDC \):
- In triangle \( BCD \):
\( \angle BDC = 180^\circ - \angle B - \angle BCD = 180^\circ - 78^\circ - 51^\circ = 51^\circ \)

4. Calculate Angle \( CBE \):
- In triangle \( CBE \):
\( \angle CBE = 24^\circ \)
- Calculate angle \( CEB \):
\( \angle CEB = 180^\circ - \angle C - \angle CBE = 180^\circ - 78^\circ - 24^\circ = 78^\circ \)

5. Establish Relationships:
- Since \( \angle BDC = 51^\circ \) and \( \angle CBE = 24^\circ \), we can find \( \angle CDE \).
- In triangle \( CDE \):
\( \angle CDE = \angle CBE - \angle BDC = 24^\circ - 51^\circ = -27^\circ \text{ (not possible)} \)
- Instead, we need to calculate \( \angle BDE \) and \( \angle CDE \) correctly.

6. Calculate Angle \( BDE \):
- Since \( \angle BDC = 51^\circ \) and \( \angle CBE = 24^\circ \):
\( \angle BDE = 180^\circ - \angle CBE - \angle BDC = 180^\circ - 24^\circ - 51^\circ = 105^\circ \)

7. Calculate Angle \( CDE \):
- Now, we can find \( \angle CDE \):
\( \angle CDE = \angle BDE - \angle BDC = 105^\circ - 51^\circ = 54^\circ \)

Final Answer:
\( \angle CDE = 54^\circ \)