In a school, 300 students were surveyed. The survey showed that 186 students liked watching cricket match while the rest disliked it. Out of these students, if one student is chosen at random, what is the probability that the chosen student :
(i) likes watching cricket match?
(ii) dislikes watching cricket match?
The correct Answer is:(i) 3150, (ii) 1950
To solve the problem step by step, we will calculate the probability of two events: (i) a student liking cricket matches and (ii) a student disliking cricket matches.
1. Identify the total number of students surveyed:
Total number of students=300
2. Identify the number of students who like watching cricket matches:
Number of students who like cricket=186
3. Calculate the number of students who dislike watching cricket matches:
Number of students who dislike cricket=Total students−Students who like cricket
=300−186=114
4. Calculate the probability that a randomly chosen student likes watching cricket matches:
P(likes cricket)=Number of students who like cricketTotal number of students
=186300
To simplify this fraction, we can divide both the numerator and the denominator by their greatest common divisor (GCD), which is 6:
=186÷6300÷6=3150
5. Calculate the probability that a randomly chosen student dislikes watching cricket matches:
P(dislikes cricket)=Number of students who dislike cricketTotal number of students
=114300
Again, we simplify this fraction by dividing both the numerator and the denominator by their GCD, which is 6:
=114÷6300÷6=1950
Final Answers:
(i) The probability that the chosen student likes watching cricket match is 3150.
(ii) The probability that the chosen student dislikes watching cricket match is 1950.
Total number of students=300
Number of students who like cricket=186
Number of students who dislike cricket=Total students−Students who like cricket
=300−186=114
P(likes cricket)=Number of students who like cricketTotal number of students
=186300
To simplify this fraction, we can divide both the numerator and the denominator by their greatest common divisor (GCD), which is 6:
=186÷6300÷6=3150
P(dislikes cricket)=Number of students who dislike cricketTotal number of students
=114300
Again, we simplify this fraction by dividing both the numerator and the denominator by their GCD, which is 6:
=114÷6300÷6=1950
(i) The probability that the chosen student likes watching cricket match is 3150.
Topper's Solved these Questions
- PROBABILITYBook:ICSEChapter:PROBABILITYExercise:EXERCISE 25
Explore 5 Videos
- PROBABILITYBook:ICSEChapter:PROBABILITYExercise:EXAMPLE
Explore 7 Videos
- PERIMETER AND AREA Book:ICSEChapter:PERIMETER AND AREA Exercise:TRY THIS
Explore 41 Videos
- PROFIT AND LOSS Book:ICSEChapter:PROFIT AND LOSS Exercise:EXERCISE 10
Explore 18 Videos
Similar Questions
In a survery of 200 employees of a company, it was found that 89 liked the lunch packs provided by the Company while the rest did not. Out of these employees, if one employee is chosen at random, what is the probability that the chosen employee:
(i) likes the lunch pack? (ii) dislikes the lunch pack?
View SolutionA survey shows that 69% students like mathematics, whereas 75% like chemistry. If x% students like both the subjects, then the maximum value of x is
View Solution
Knowledge Check

The table above shows the distribution of the gender and the language studied of the 30 students in an after-school language program. If a student is chosen at random, what is the probability that the student will be either a boy studying French or a girl studying Spanish?A330B1030C1130D1330A recent survey reported that 60 percent of the students at a high school are girls and 65 percent of girls at this school play a sport. If a student at this high school were selected at random, what is the probability that the student is a girl who plays a sport?
A0.1B0.21C0.32D0.42In a college 30 % students fail in physics , 25 % fail in mathematics and 10 % fail in both subjects .One student is chosen at random . The probability that she fails in physics if she has failed in mathematics is
A110B25C920D13
In a college, 70% students pass in Physics, 75% pass in Mathematics and 10% students fail in both. One student is chosen at random. What is the probability that:
He passes in Physics and Mathematics.
View SolutionA survey of 300 girls of a school was conducted and it was found that 108 girls like tea and 192 dislike it. Out of these girls one girl is selected at random. What is the probability that the selected girl (i) likes tea (ii) does not like tea.
View SolutionIn a college, 70% students pass in Physics, 75% pass in Mathematics and 10% students fail in both. One student is chosen at random. What is the probability that:
He passes in Mathematics given that he passes in Physics.
View SolutionIn a college, 70% students pass in Physics, 75% pass in Mathematics and 10% students fail in both. One student is chosen at random. What is the probability that:
He passes in Physics given that he passes in Mathematics.
View Solution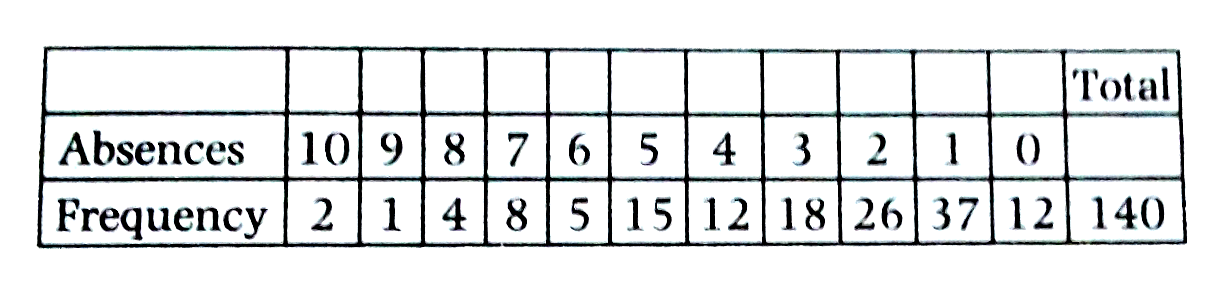
The student attendance record for a class in a one-semester course is shown above. If 2 students are chosen at random, what is the probability , to the nearest hundredth , that both students have fewer than 2 absences ?
View Solution

