AB is a line of fixed length, 6 units, joining the points A (t, 0) and B which lies on the positive y-axis. P is a point on AB distant 2 units from A. Express the co-ordinates of B and P in terms of t. Find the locus of P as t varies.
The correct Answer is:B(0,√36−t2),P(2t3,√36−t23),x2+4y2=16
To solve the problem step by step, we will follow the given information and derive the required coordinates and locus of point P.
Step 1: Identify the coordinates of points A and B
- Point A is given as A(t,0).
- Point B lies on the positive y-axis, so we can denote its coordinates as B(0,k), where k>0.
Step 2: Use the distance formula to find the relationship between A and B
The length of line segment AB is given as 6 units. Using the distance formula:
AB=√(t−0)2+(0−k)2=6
This simplifies to:
√t2+k2=6
Squaring both sides, we get:
t2+k2=36(1)
Step 3: Determine the coordinates of point P
Point P is located on line segment AB and is 2 units away from A. Since AB is 6 units long, the distance from P to B will be 6−2=4 units.
Using the section formula, since P divides AB in the ratio 1:2 (1 part from A to P and 2 parts from P to B), the coordinates of P can be calculated as follows:
P(1⋅0+2⋅t1+2,1⋅k+2⋅01+2)=P(2t3,k3)
Step 4: Express k in terms of t using equation (1)
From equation (1):
k2=36−t2
Taking the square root:
k=√36−t2
Step 5: Substitute k into the coordinates of P
Now substituting k into the coordinates of P:
P(2t3,√36−t23)
Step 6: Find the locus of P as t varies
To find the locus of point P, we need to eliminate t from the coordinates of P. We have:
x=2t3⇒t=3x2
Substituting this into the equation for y:
y=√36−t23=√36−(3x2)23
Calculating t2:
t2=(3x2)2=9x24
Thus,
y=√36−9x243
Simplifying further:
y=13√144−9x24=16√144−9x2
Squaring both sides:
36y2=144−9x2
Rearranging gives:
9x2+36y2=144
Dividing through by 144:
x216+y24=1
This is the equation of an ellipse.
Final Answer:
The locus of point P as t varies is given by:
x216+y24=1
- Point A is given as A(t,0).
- Point B lies on the positive y-axis, so we can denote its coordinates as B(0,k), where k>0.
The length of line segment AB is given as 6 units. Using the distance formula:
AB=√(t−0)2+(0−k)2=6
This simplifies to:
√t2+k2=6
Squaring both sides, we get:
t2+k2=36(1)
Point P is located on line segment AB and is 2 units away from A. Since AB is 6 units long, the distance from P to B will be 6−2=4 units.
P(1⋅0+2⋅t1+2,1⋅k+2⋅01+2)=P(2t3,k3)
From equation (1):
k2=36−t2
Taking the square root:
k=√36−t2
Now substituting k into the coordinates of P:
P(2t3,√36−t23)
To find the locus of point P, we need to eliminate t from the coordinates of P. We have:
x=2t3⇒t=3x2
Substituting this into the equation for y:
y=√36−t23=√36−(3x2)23
Calculating t2:
t2=(3x2)2=9x24
Thus,
y=√36−9x243
Simplifying further:
y=13√144−9x24=16√144−9x2
Squaring both sides:
36y2=144−9x2
Rearranging gives:
9x2+36y2=144
Dividing through by 144:
x216+y24=1
This is the equation of an ellipse.
The locus of point P as t varies is given by:
x216+y24=1
Topper's Solved these Questions
- THE STRAIGHT LINE BOOK - ICSECHAPTER - THE STRAIGHT LINE EXERCISE - EXERCISE 16 (j)
10 Videos
- THE STRAIGHT LINE BOOK - ICSECHAPTER - THE STRAIGHT LINE EXERCISE - CHAPTER TEST
15 Videos
- THE STRAIGHT LINE BOOK - ICSECHAPTER - THE STRAIGHT LINE EXERCISE - EXERCISE 16 (h)
11 Videos
- STRAIGHT LINES BOOK - ICSECHAPTER - STRAIGHT LINES EXERCISE - Multiple Choice Questions
46 Videos
- TRIGONOMETRIC FUNCTIONBOOK - ICSECHAPTER - TRIGONOMETRIC FUNCTIONEXERCISE - MULTIPLE CHOICE QUESTIONS
44 Videos
Similar Questions
A is a point on x- axis, and point B (5,-4) and AB = 5 units find the co-ordinates of A.
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the
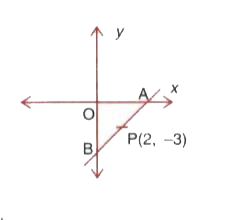
co-ordinates of A and B.
View SolutionIn the given figure, P (4, 2) is mid-point of line segment AB. Find the co-ordinates of A and B.
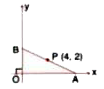
View SolutionThe line joining the points A (-3, -10) and B (-2, 6) is divided by the point P such that PBAB=15. Find the co-ordinates of P.
View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
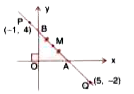
The co-ordinates of A and B.
View SolutionFind the co-ordinates of the points on y axis which are at a distance of 5√2 units from the point (5,8)
View SolutionFind the equation of a line passing through the points (7,−3)and(2,−2). If this line meets x-axis at point P and y-axis at point Q, find the co-ordinates of points P and Q.
View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
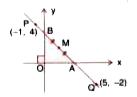
The co-ordinates of M.
View SolutionPoint (x,4) lies on the line segment joining the points A (-5, 8) and B (4,-10) Find the ratio in which point P divides the line segment AB. Also find the value of x?
View SolutionGiven a line segment AB joining the points A (-4, 6) and B (8, -3). Find :
(i) the ratio in which AB is dividend by the Y-axis.
View Solution
