A point O lies inside a square ABCD such that OA=3, OB=4 and OD=5, find the value of OC.
A)3√3
B)6.67
C)3√2
D)4√2
The correct Answer is:D
To solve the problem, we will use the property of a point inside a square. The property states that for any point O inside a square ABCD:
OA2+OC2=OB2+OD2
Given:
- OA=3
- OB=4
- OD=5
We need to find OC.
1. Calculate OA2:
OA2=32=9
2. Calculate OB2:
OB2=42=16
3. Calculate OD2:
OD2=52=25
4. Substitute the values into the property:
Using the property OA2+OC2=OB2+OD2:
9+OC2=16+25
5. Simplify the right side:
16+25=41
So, we have:
9+OC2=41
6. Isolate OC2:
OC2=41−9
OC2=32
7. Calculate OC:
OC=√32=√16×2=4√2
Thus, the value of OC is 4√2.
Final Answer:
OC=4√2
- OA=3
- OB=4
- OD=5
OA2=32=9
OB2=42=16
OD2=52=25
Using the property OA2+OC2=OB2+OD2:
9+OC2=16+25
16+25=41
So, we have:
9+OC2=41
OC2=41−9
OC2=32
OC=√32=√16×2=4√2
OC=4√2
Topper's Solved these Questions
Similar Questions
O is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
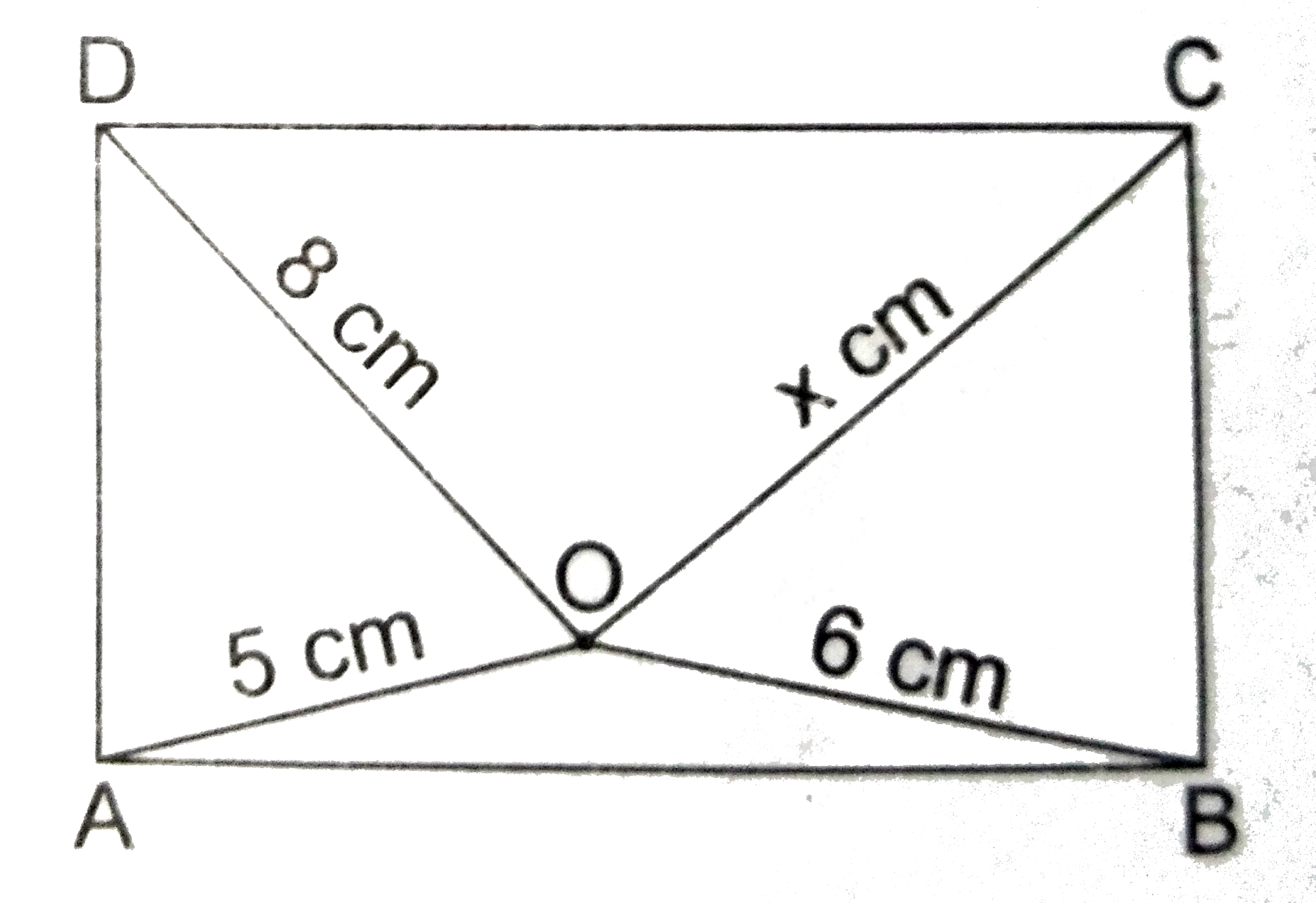
DEDUCTION In the given figure, O is a point inside a rectangle ABCD such that OB=6cm,OD=8cmandOA=5cm, find the length of OC.
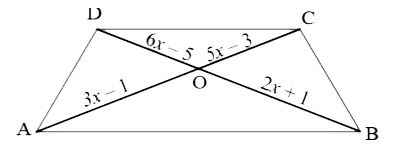
View SolutionIn the given fig., AB || DC and diagonals AC and BD intersects at O. If OA =3x-1 and OB =2x + 1, OC = 5x-3 and OD =6x-5, find the value of x.
View Solution
Knowledge Check
A point O lies inside a square ABCD such that OB=7 and OD=6, OC=2 find the value of OA?
A9B6C5D12OABC is a parallelogram such that OA=a,OB=bandOC=c, then the value →OA.→BA is
Aa2+3b2+c22Ba2−b2+3c22Ca2+3b2−c22D3a2+b2−c22Let O be an interior point of triangle ABC, such that 2−−→OA+3−−→OB+4−−→OC=0, then the ratio of the area of ΔABC to the area of ΔAOC is
A3:1B3:2C2:1D4:3
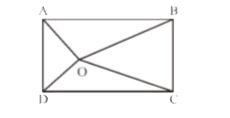
O is a point situated inside a rectangle ABCD. If sides OA, OC and OD are 6 cm, 8 cm and 6 cm respectively, then find the value of OB-
View SolutionIf O is a point within a quadrilateral ABCD, show that OA+OB+OC+OD>AC+BD.
View SolutionIn figure OAOC=OBOD=12and AB=5cm. Find the value of DC
View SolutionABCD is a quadrilateral whose diagonals intersect each other at the point O such that OA=OB=OD.If∠OAB=30∘, then the measure of ODA is :
View SolutionIn a parallelogram ABCD diagonals AC and BD intersect at O and AC =12.6 cm and BD = 9.4 cm. Find the measures of OC and OD.
View Solution
