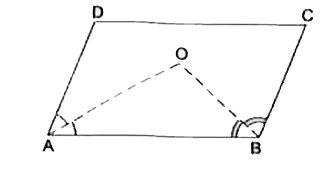
In a parallelogram ABCD, the bisectors of ∠Aand∠B intersect each other at point P. Prove that ∠APB=90∘.
90∘
60∘
120∘
data insufficient
The correct Answer is:A
Step by step video, text & image solution for In a parallelogram ABCD, the bisectors of angleA and angleB intersect each other at point P. Prove that angleAPB=90^(@). by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
In a ΔABC, the bisectors of ∠Band∠C intersect each other point O. Then∠BOC is ?
A∠BOC=180∘+12∠A.B∠BOC=90∘+12∠A.C∠BOC=180∘−12∠A.D∠BOC=90∘−12∠A.In parallelogram ABCD, bisectors of angles A and B intersect each other at "O" the value of angle AOB is.
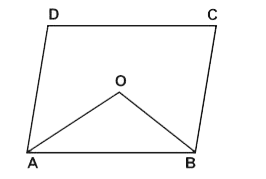 A90∘B30∘C60∘D120∘
A90∘B30∘C60∘D120∘In a parallelogram ABCD, the bisectors of ∠Aand∠B intersect each other at point P. Prove that ∠APB=90∘.
A90∘B60∘C120∘Ddata insufficient
In a parallelogram ABCD, the bisector of ∠A bisects the line Bcat point X. Prove that AD = 2AB.
View SolutionIn the figure the bisectors of ∠P and ∠Q intersect to each other at a point R. Prove that ∠PRQ=90∘.
View SolutionIn a parallelogram ABCD, AX and CY are the bisectors of ∠Aand∠C respectively. Prove that AX||CY.
View SolutionTriangle ABC is an isosceles triangle with AB=AC. Bisectors of ∠Band∠C intersect each other at O. join A−O and prove that
OB=OC
View SolutionIn a parallelogram ABCD, bisectors of consecutive angles A and B intersect at P. Find the measure of ∠APB :
View Solution