Which of the following is true, in the given figure, where AD is the altitude to the hypotenuse of a right angled △ABC?
△CAD and △ABD are similar
△CDA and △ADB are congruent
△ADB and △CAB are similar
Select the correct answer using the codes given below :
A)1 and 2
B)2 and 3
C)1 and 3
D)1, 2 and 3
The correct Answer is:C
To solve the problem, we need to analyze the relationships between the triangles formed when an altitude is drawn from vertex A to the hypotenuse BC in right triangle ABC.
1. Identify the Triangles:
- We have triangle ABC, where angle A is the right angle (90 degrees).
- The altitude AD is drawn from vertex A to the hypotenuse BC, creating two smaller triangles: triangle ABD and triangle ACD.
2. Determine Angles in Triangle ABD:
- In triangle ABD:
- Angle ADB = 90 degrees (since AD is the altitude).
- Let angle CAB = θ (this is one of the angles in triangle ABC).
- Therefore, angle ABD = 90 - θ = α (the other angle in triangle ABC).
3. Determine Angles in Triangle ACD:
- In triangle ACD:
- Angle ADC = 90 degrees (since AD is the altitude).
- Angle ACD = θ (same as angle CAB).
- Therefore, angle CAD = 90 - θ = α.
4. Check Similarity of Triangle CAD and Triangle ABD:
- Triangle CAD has angles: θ, α, and 90 degrees.
- Triangle ABD has angles: θ, α, and 90 degrees.
- Since both triangles have the same angles, they are similar by AA (Angle-Angle) similarity criterion.
5. Check Congruence of Triangle CDA and Triangle ADB:
- Triangle CDA has angles: θ, 90 degrees, and α.
- Triangle ADB has angles: θ, 90 degrees, and α.
- While they are similar, we cannot conclude they are congruent unless their corresponding sides are equal. Therefore, this statement is false.
6. Check Similarity of Triangle ADB and Triangle CAB:
- Triangle ADB has angles: θ, α, and 90 degrees.
- Triangle CAB has angles: θ, α, and 90 degrees.
- Since both triangles have the same angles, they are also similar by AA similarity criterion.
Conclusion:
- The correct statements are:
- Triangle CAD and triangle ABD are similar (True).
- Triangle CDA and triangle ADB are congruent (False).
- Triangle ADB and triangle CAB are similar (True).
Thus, the correct answer is options 1 and 3.
- We have triangle ABC, where angle A is the right angle (90 degrees).
- The altitude AD is drawn from vertex A to the hypotenuse BC, creating two smaller triangles: triangle ABD and triangle ACD.
- In triangle ABD:
- Angle ADB = 90 degrees (since AD is the altitude).
- Let angle CAB = θ (this is one of the angles in triangle ABC).
- Therefore, angle ABD = 90 - θ = α (the other angle in triangle ABC).
- In triangle ACD:
- Angle ADC = 90 degrees (since AD is the altitude).
- Angle ACD = θ (same as angle CAB).
- Therefore, angle CAD = 90 - θ = α.
- Triangle CAD has angles: θ, α, and 90 degrees.
- Triangle ABD has angles: θ, α, and 90 degrees.
- Since both triangles have the same angles, they are similar by AA (Angle-Angle) similarity criterion.
- Triangle CDA has angles: θ, 90 degrees, and α.
- Triangle ADB has angles: θ, 90 degrees, and α.
- While they are similar, we cannot conclude they are congruent unless their corresponding sides are equal. Therefore, this statement is false.
- Triangle ADB has angles: θ, α, and 90 degrees.
- Triangle CAB has angles: θ, α, and 90 degrees.
- Since both triangles have the same angles, they are also similar by AA similarity criterion.
- The correct statements are:
- Triangle CAD and triangle ABD are similar (True).
- Triangle CDA and triangle ADB are congruent (False).
- Triangle ADB and triangle CAB are similar (True).
Topper's Solved these Questions
Similar Questions
Knowledge Check
The hypotenuse of a right-angled isosceles triangle is 5 cm. The area of the triangle is (a) 5 cm2 (b) 6.25 cm2 (c) 6.5 cm2 (d) 12.5 cm2
A5 cm2B6.25 cm2C6.5 cm2D12.5 cm2Altitude on the hypotenuse of a right angled triangle triangle divides it in two parts of lengths 4 cm and 9 cm. Find the length of the altitude.
A9 cmB4 cmC6 cmD2√6 cm
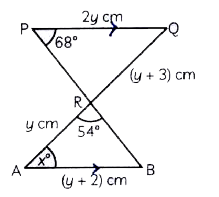
Given that △PQR is similar to △BAR, find the value of x:
View SolutionIn the figure given below, M is the mid-point of AB and ∠DAB=∠CBAand∠AMC=∠BMD. Then the triangle ADM is congruent to the triangle BCM by
View SolutionABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD. Which of the following statements is/are correct?
1. The area of triangle ABC is equal to four times the area of triangle BED.
2. The area of triangle ADC is twice the area of triangle BED.
Select the correct answer using the code given below.
View SolutionIn a triangle ABC, having AD is median and area of triangle ABD= 120m2. Find area of triangle ABC.
View SolutionConstruct a triangle similar to a given triangle ABC with its sides equal to 53 of the corresponding sides of the triangle ABC (i.e., of scale factor 53)
View SolutionIn a right-angled triangle ABC, if angle B=90°, then which of the following is true?
View Solution