The correlation coefficient between x and y is 0.6. If the variance of x is 225, th variance of y is 400, mean of x is 10 and mean of y is 20, find the equation of two regression lines.
The correct Answer is:Regression equation of y on x ; y=45x=12, Regression equation x on y : x=920y+1
Step by step video, text & image solution for The correlation coefficient between x and y is 0.6. If the variance of x is 225, th variance of y is 400, mean of x is 10 and mean of y is 20, find the equation of two regression lines. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The correlation coefficient between x and y is 0.6. If the variance of x is 225 , the variance of y is 400 , mean of x is 10 and mean of y is 20 , find
(i) the equations of two regression lines.
(ii) the expected value of y when x = 2
View SolutionThe mean of 5 observations 1,2,6,x and y is 4.4 and their variance is 8.24 , then x+y is
View Solution
Knowledge Check
If byx=−14, mean of x = 3 and mean of y = 3, then regression equation y on x is
A4x+y=15Bx+4y=15Cx+y=15Dnone of the aboveIf coefficient of correlation is -0.6, standard deviation of x is 5 and variance of y is 16, then what is the co-variance of x and y?
A0.75B0.48C-0.03D-0.75The regression equation of x on y is 9x−2y−38=0. If mean of x series is 6, then mean of y series is
Aa) 8Bb) 6Cc) 10Dd) None of these
The coefficient of correlation between the values denoted by x and y is 0.5. The standard deviation of x is 5 and that of y is 4. Find the angle between the lnes of regression.
View SolutionYou are given the following data:
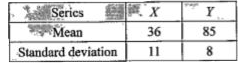
Correlation coefficient between x and y=0.66. Find the equations of the lines of regression.
View SolutionThe two lines of of regressions are x+2y−5=0 and 2x+3y−8=0 and the variance of x is 12. Find the variance of y and the coefficient of correlation.
View SolutionThe two lines of regression are x+2y−5=0and2x+3y−8=0 and the variance of x is 12. Find the variance of y and the coefficient of correlation.
View SolutionTwo lines of regressions are represented by 4x+10y=9 and 6x+3y=4. Find the line of regression y on x.
View Solution

