The Spearman's rank correlation coefficient =911, given ∑d2=30 . Find the number of observation.
The correct Answer is:10
To find the number of observations (N) given the Spearman's rank correlation coefficient and the sum of squared differences, we can follow these steps:
Step 1: Write down the formula for Spearman's rank correlation coefficient (P).
The formula is:
P=1−6Σd2N(N2−1)
where Σd2 is the sum of the squared differences of ranks, and N is the number of observations.
Step 2: Substitute the known values into the formula.
Given:
- P=911
- Σd2=30
Substituting these values into the formula:
911=1−6×30N(N2−1)
Step 3: Simplify the equation.
Rearranging the equation gives:
6×30N(N2−1)=1−911
Calculating 1−911:
1−911=11−911=211
So, we have:
180N(N2−1)=211
Step 4: Cross-multiply to eliminate the fraction.
Cross-multiplying gives:
180×11=2×N(N2−1)
Calculating 180×11:
1980=2N(N2−1)
Step 5: Divide both sides by 2.
990=N(N2−1)
Step 6: Rewrite the equation.
We can rewrite this as:
N3−N−990=0
Step 7: Find integer solutions for N.
We can try different integer values for N to find a solution. Testing N=10:
103−10−990=1000−10−990=0
Thus, N=10 is a solution.
Conclusion:
The number of observations N is 10.
---
The formula is:
P=1−6Σd2N(N2−1)
where Σd2 is the sum of the squared differences of ranks, and N is the number of observations.
Given:
- P=911
- Σd2=30
911=1−6×30N(N2−1)
Rearranging the equation gives:
6×30N(N2−1)=1−911
Calculating 1−911:
1−911=11−911=211
So, we have:
180N(N2−1)=211
Cross-multiplying gives:
180×11=2×N(N2−1)
Calculating 180×11:
1980=2N(N2−1)
990=N(N2−1)
We can rewrite this as:
N3−N−990=0
We can try different integer values for N to find a solution. Testing N=10:
103−10−990=1000−10−990=0
Thus, N=10 is a solution.
The number of observations N is 10.
Topper's Solved these Questions
Similar Questions
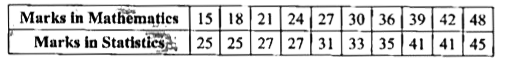
Find Spearman's rank correlation coefficient .
View SolutionFind the Spearmen 's rank correlation coeffcient ,given : n=10,∑∣∣dx−dy∣∣2=30
View SolutionCalculate the Spearman's rank correlation coefficient for the following data and interpret the result.

View SolutionCalculate Spearman's rank correlation coefficient between the marks in Mathematics and Accountancy by 9 students.

View SolutionCalculate spearman's rank correlation coefficient between the advertisement cost and sales cost of making a Maggie. The following data is given below.
Advertisement cost (₹ in thousand)40323832506055Sales (₹ in lakhs)32354340425070
View SolutionYou are given the following data:
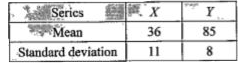
Correlation coefficient between x and y=0.66. Find the equations of the lines of regression.
View SolutionThe sum of three times a number and 11 is 32. Find the number.
View SolutionTwo numbers are in the ratio 9 : 13 and their sum is 176 . Find the number .
View SolutionWhile calculating correlation coefficient between two variables x and y for 30 pairs of observation, the students observed the following results:
Σx=135,Σx2=680,Σy=110,Σy2=485andΣxy=530
On rechecking, it was found that he had wrongly copied one pir as (5,8) whereas value is (7,9) calculate the correct correlation coefficient between x and y.
View SolutionIf the mean of 12 observations is 9, find the sum of the 12 observations.
View Solution
