Write down the expression for the average K.E. and average P.E. of a harmonic oscillator. How are they related ?
To solve the question, we need to derive the expressions for the average kinetic energy (K.E.) and average potential energy (P.E.) of a harmonic oscillator and then discuss their relationship.
Step 1: Average Kinetic Energy of a Harmonic Oscillator
The average kinetic energy (K.E.) of a harmonic oscillator can be derived from its motion. The kinetic energy at any point in time is given by:
K.E.=12mv2
Where:
- m is the mass of the oscillator,
- v is the velocity of the oscillator.
For a harmonic oscillator, the velocity v can be expressed in terms of angular frequency ω and amplitude a:
v=ω√a2−x2
Where x is the displacement from the mean position. The average kinetic energy over one complete cycle can be calculated as:
Average K.E.=1T∫T0K.E.dt
Where T is the period of oscillation. After performing the integration, the average kinetic energy is found to be:
Average K.E.=14mω2a2
Step 2: Average Potential Energy of a Harmonic Oscillator
The average potential energy (P.E.) of a harmonic oscillator can be derived similarly. The potential energy at any point in time is given by:
P.E.=12kx2
Where:
- k is the spring constant.
For a harmonic oscillator, the spring constant k is related to the angular frequency ω by:
k=mω2
Thus, the potential energy can be expressed as:
P.E.=12mω2x2
The average potential energy over one complete cycle can be calculated similarly:
Average P.E.=1T∫T0P.E.dt
After performing the integration, the average potential energy is found to be:
Average P.E.=14mω2a2
Step 3: Relationship Between Average K.E. and Average P.E.
From the expressions derived, we can see that:
Average K.E.=14mω2a2
Average P.E.=14mω2a2
This shows that the average kinetic energy is equal to the average potential energy for a harmonic oscillator:
Average K.E.=Average P.E.
Conclusion
In conclusion, the average kinetic energy and average potential energy of a harmonic oscillator are both given by the same expression, and they are equal to each other.
---
The average kinetic energy (K.E.) of a harmonic oscillator can be derived from its motion. The kinetic energy at any point in time is given by:
- m is the mass of the oscillator,
- v is the velocity of the oscillator.
The average potential energy (P.E.) of a harmonic oscillator can be derived similarly. The potential energy at any point in time is given by:
- k is the spring constant.
From the expressions derived, we can see that:
Average P.E.=14mω2a2
In conclusion, the average kinetic energy and average potential energy of a harmonic oscillator are both given by the same expression, and they are equal to each other.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - LONG ANSWER QUESTIONS3videos
OSCILLATIONS
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SHORT ANSWER QUESTIONS47videos
OSCILLATIONS
- BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - ADDITIONAL SOLVED PROBLEMS11videos
OSCILLATIONS
- BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)19videos
MOTION IN FLUIDS
- BOOK - ICSECHAPTER - PROPERTIES OF MATTEREXERCISE - MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS12videos
PROPERTIES OF MATTER
Similar Questions
Write down the expression for the stationary wave.
View SolutionDerive an expression for the mean K.E. of a gas molecule.
View SolutionDerive an expression for the P.E. and K.E. of a body executing shm.
View SolutionWrite down a relation expressing the mechanical advantage of a lever.
View SolutionWrite down the structures of the (E) and (F).
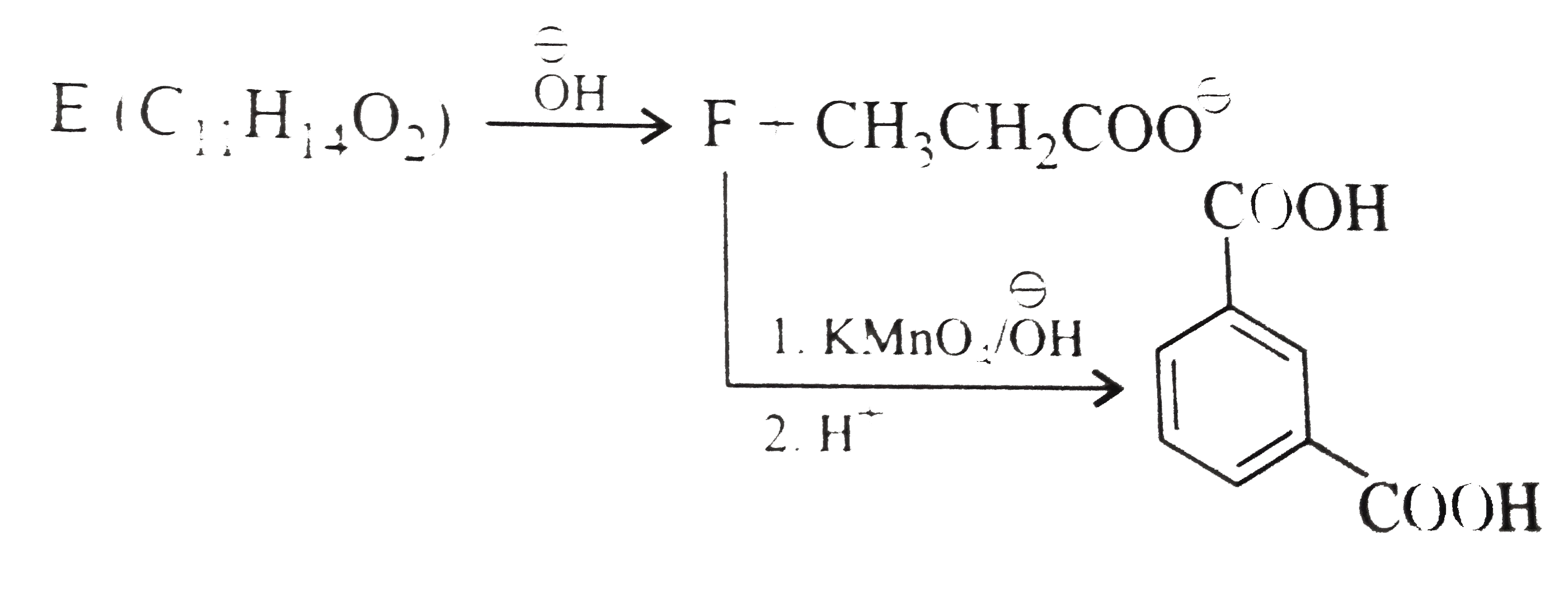 .View Solution
.View SolutionWrite down the expression for the period of oscillation of a light piece of cork floating in a liquid .
View SolutionWrite down the expression for the nth harmonic in (i) closed pipe (ii) an open pipe.
View SolutionWrite down the expression for the period of oscillation of a mass attached to (i) a horizontal spring and (ii) a vertical spring.
View SolutionThe graph showing the variation of K.E. or P.E. with displacement of a harmonic oscillator is a parabola, but that of total energy with displacement is a straight line. Why?
View SolutionThe ratio of average translational K.E. and average rotational K.E. of a linear polyatomic molecule at temperature T is:
View Solution
