A trolley of mass 3.0 kg is connected to two identical springs each of force constant 600 Nm as shown in Fig. If the trolley is displaced from its equilibrium position by 5.0 cm and released, what is (a) period of oscillation, (b) the maximum speed of the trolley, (c) how much is the total energy dissipated as heat by the time the trolley comes to rest due to damping force ?

Let the trolley be displaced by x from the mean position. One spring stretches and the other springs gets compressed by the same amount. So restoring force is doubled or the spring constant is 2k where k =600Nm−1
m = 3.0 kg , amlitude a=5.0×10−2m
(a) T=2π√m2k=2×3.14√32×600=0.314s
(b) Maximum speed =vman=aω=a√2km
=5.0×10−2√12003.0=1.0ms−1
(c) The initial energy is converted into heat
Total energy = Maximum K.E. =12mv2max
=12×3.0×(1.0)2=1.5J
Topper's Solved these Questions
- OSCILLATIONS Book:ICSEChapter:OSCILLATIONS Exercise:SHORT ANSWER QUESTIONS WITH ANSWER
Explore 20 Videos
- OSCILLATIONS Book:ICSEChapter:OSCILLATIONS Exercise:LONG ANSWER QUESTIONS
Explore 3 Videos
- OSCILLATIONS Book:ICSEChapter:OSCILLATIONS Exercise:SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
Explore 2 Videos
- MOTION IN FLUIDS Book:ICSEChapter:MOTION IN FLUIDS Exercise:SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
Explore 19 Videos
- PROPERTIES OF MATTERBook:ICSEChapter:PROPERTIES OF MATTERExercise:MODULE 4 ( TEMPERATURE ) UNSOLVED PROBLEMS
Explore 12 Videos
Similar Questions
A trolley of mass 3.0kg is connected to two identical spring each of force constant 600Nm−1 as shown in figure. If the trolley is displaced from its equilibrium position by 5.0 cm and released, what is
(a) the period of ensuing oscillation?
(b) the maximum speed of trolley?
(c) How much is the total energy dissipated as heat by the time the trolley comes to rest due to damping forces?

View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximum speed of the trolley is
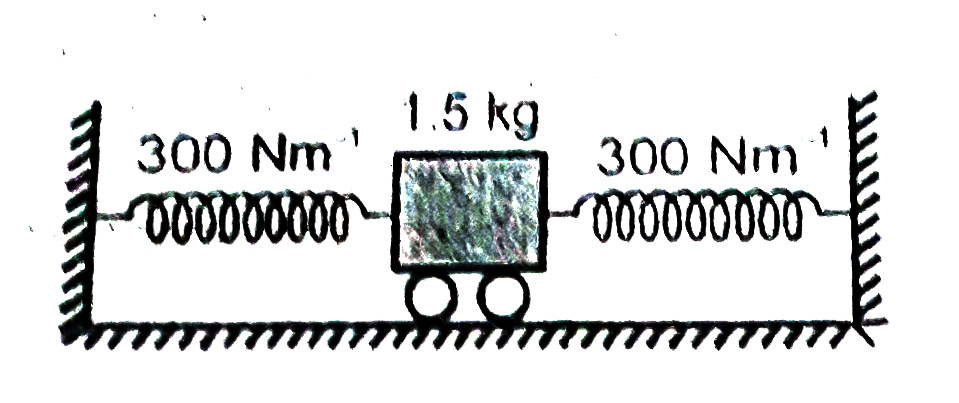
View SolutionA 2.5 kg collar attached to a spring of foce constant 1000 Nm−1 slides without friction on a horizontal rod. The collar is displaced from its equilibrium position by 5.0 cm and released. Calculate (i) the period of oscillation (ii) the maximum speed of the collar and (iii) the maximum acceleration of the collar.
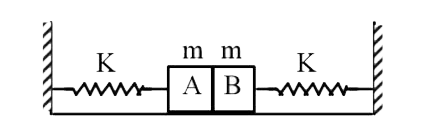
View SolutionTwo blocks each of mass m are connected with springs each of force constant K as shown in fig. The mass A is displaced to the left & B to the right by the same amount and released then the time period of oscillation is -
View SolutionA particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is

View SolutionA particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is

View SolutionA 5 kg collar is attached to a spring of spring constant 500Nm−1 . It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10 cm and released. Calculate (a) The period of oscillations (b) The maximum speed and (c) maximum acceleration of the collar.
View SolutionA trolley of mass 3.0kg is connected to two identical springs each of force constant 600Nm−1as shown in figure 13.32 (amplitude=5cm)
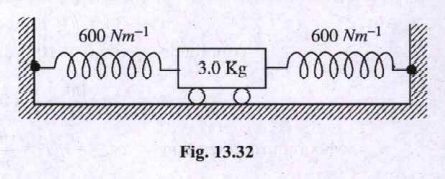
Problem (a) period of oscillation
Problem (b) the max speed of trolley.
If the spring in the problem are replaced by rubber bands, what is the answer to the question (a) and (b) in the problem if K of rubber band is 600Nm−1 during extensions.
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution