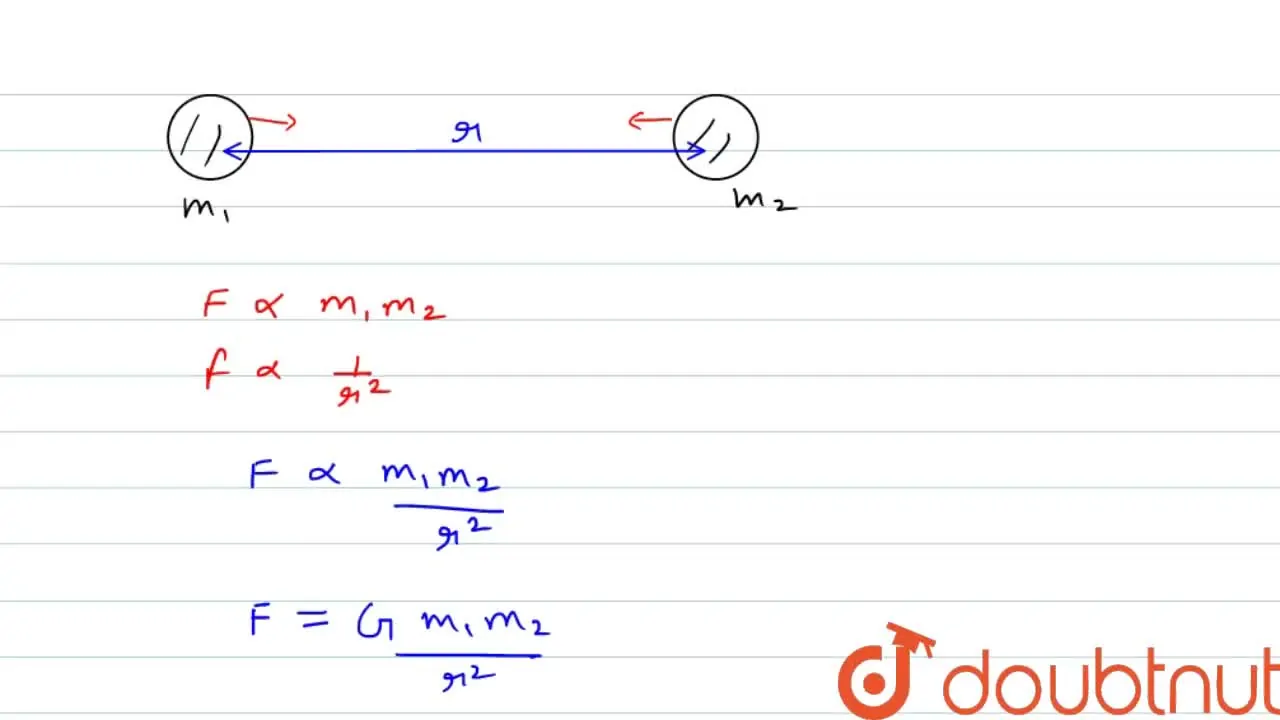
Give the quantities for which the following are the dimensions:
The correct Answer is:G
Step by step video, text & image solution for Give the quantities for which the following are the dimensions: M^(-1)L^(3)T^(-2) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Related Playlists
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM FINDING THE DIMENSION OF A PHYSICAL QUANTITY)3videos
DIMENSIONS
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM DERIVATION OF FORMULAE USING DIMENSIONS)5videos
DIMENSIONS
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - VERY SHORT ANSWER QUESTIONS5videos
DIMENSIONS
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS50videos
COMPETITION CARE UNIT
- BOOK - ICSECHAPTER - DYNAMICSEXERCISE - SHORT ANSWER QUESTIONS WITH ANSWERS12videos
DYNAMICS
Similar Questions
Give the quantities for which the following are the dimensions:
M1L2View SolutionGive the quantities for which the following are the dimensions:
M1L−1T−2View SolutionGive the quantities for which the following are the dimensions:
M1T−2View SolutionGive the quantities for which the following are the dimensions:
M0L0T−2View SolutionGive the quantities for which the following are the dimensions:
M0L0T0View SolutionWhich of the following quantity has dimensional formula as (ML−1T−2)?
View SolutionThe physical quantity having the dimensions [M−1L−3T3A2] is
View SolutionWhich physical quantities have the same dimensions of ML−1T−2?
View SolutionThe physical quanitity the dimensions [M1L2T−3A−1] is
View SolutionWhich of the following pairs has quantities of the same dimensions?
View Solution