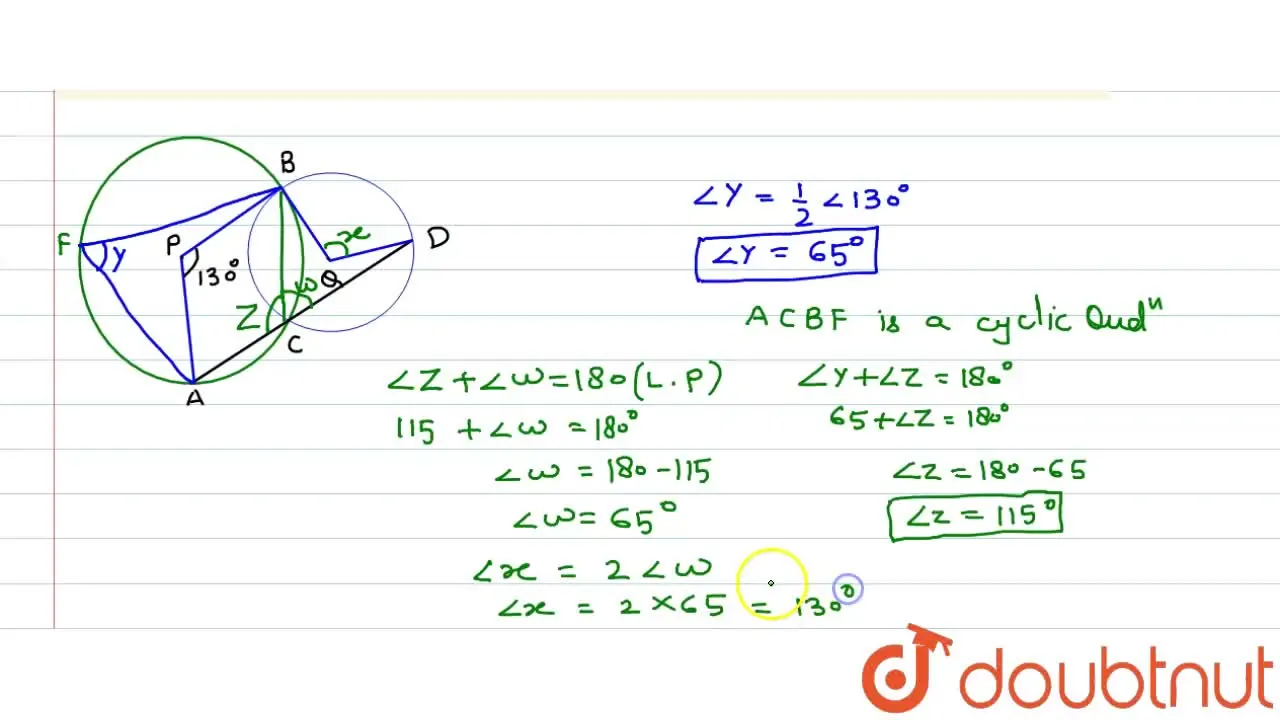
Two circles with centres P and Q intersect at B and C, A, D are points on the circles with centres P and Q respectively such that A, C, D are colliner. If ∠APB=130∘,and∠BQD=x∘, then the value of x is :
65
130
195
135
The correct Answer is:B
Step by step video, text & image solution for Two circles with centres P and Q intersect at B and C, A, D are points on the circles with centres P and Q respectively such that A, C, D are colliner. If angle APB = 130^(@), and angle BQD = x^(@), then the value of x is : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Related Playlists
Similar Questions
Two circles with centres P and Q intersect at B and C, A, D are points on the circles with centres P and Q respectively such that A, C, D are colliner. If ∠APB=130∘,and∠BQD=x∘, then the value of x is :
View SolutionTwo circle with centres A and B intersect at C and D. Prove that ∠ACB=∠ADB.
View SolutionIf 76 is divided into four parts proportional to 7, 5, 3, 4, then the smallest part is:
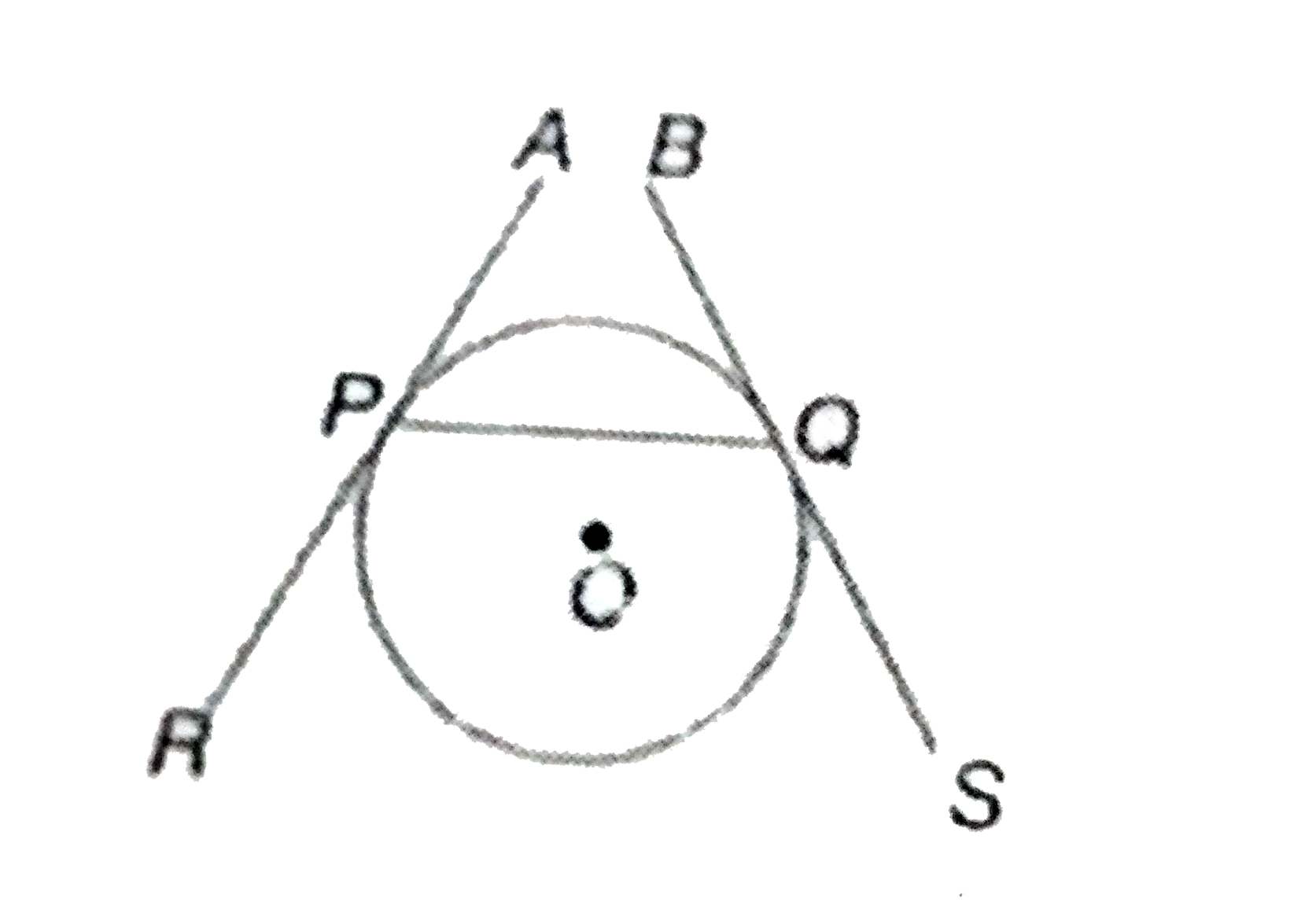
View SolutionAr and BS are the tangents to the circle, with centre O, touching at P and Q respectively and PQ is the chord. If ∠OQP=24∘,then∠RPQ= __________.
 View Solution
View SolutionAlloy A contains 40% gold and 60% silver. Alloy B contains 35% gold and 40% silver and 25% copper. Alloys A and B are mixed in the ratio of 1:4 .What is the ratio of gold and silver in the newly formed alloy is?
View SolutionThe tangents at two points A and B on the circle with centre O intersect at P. If in quadrilateral PAOB, ∠AOB:∠APB=5:1, then measure of ∠APB is :
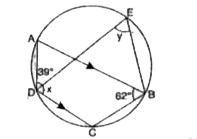
View SolutionIn the diagram, A, B, C, D, E are points on the circle. AB||DC, ∠ADE=39∘and∠ABC=62∘. Then the values of x and y respectively are :
 View Solution
View SolutionTwo circles whose centres are O and O' intersect at P. Through P, a line l parallel to OO' intersecting the circles at C and D is drawn. Prove that CD=2 OO'
View SolutionO is the centre of a circle. AC and BD are two chords of the circle intersecting each other at P. If ∠AOB=15∘and∠APB=30∘, then tan2∠APB+cot2∠COD is equal to :
View SolutionA, B and C are three points on a circle such that the angles subtended by the chords AB and AC at the centre O are 110°∘and 130∘ respectively. Then the value of ∠BAC is :
View Solution