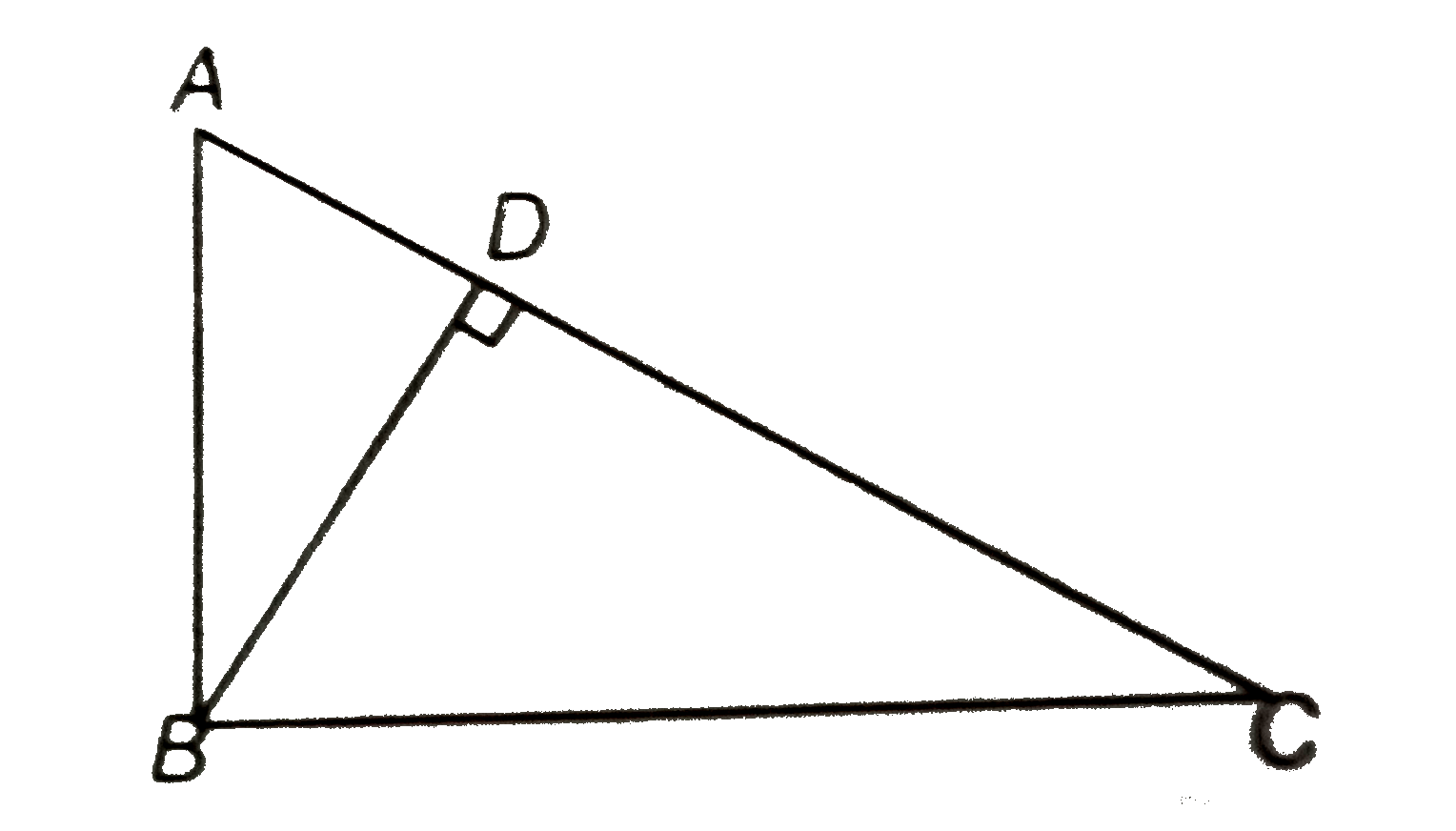
Let ABC be an acute angled triangle and CD be the altitude through C. If AB = 8 cm and CD = 6 cm, then the distance between the midpoints AD and BC is :
6
4
4.5
5
The correct Answer is:D
To solve the problem, we need to find the distance between the midpoints of segments AD and BC in triangle ABC, where CD is the altitude from point C to side AB.
1. Identify the Triangle and Given Values:
We have triangle ABC with:
- AB=8cm
- CD=6cm (the altitude from C to AB)
2. Find the Coordinates of Points A, B, and C:
We can place the triangle in a coordinate system for easier calculations:
- Let A(0,0) and B(8,0) (since AB = 8 cm lies on the x-axis).
- Point C will be directly above the midpoint of AB since CD is the altitude. The midpoint M of AB is at (4,0).
- Since CD is vertical and has a length of 6 cm, the coordinates of point C will be C(4,6).
3. Calculate Midpoints of AD and BC:
- Midpoint of AD (let's call it M1):
- A is at (0,0) and D is at (4,0) (the foot of the altitude).
- The midpoint M1 is calculated as:
M1=(0+42,0+02)=(2,0)
- Midpoint of BC (let's call it M2):
- B is at (8,0) and C is at (4,6).
- The midpoint M2 is calculated as:
M2=(8+42,0+62)=(6,3)
4. Calculate the Distance Between M1 and M2:
- The distance d between the points M1 and M2 can be calculated using the distance formula:
d=√(x2−x1)2+(y2−y1)2
- Substituting the coordinates of M1 and M2:
d=√(6−2)2+(3−0)2=√42+32=√16+9=√25=5cm
Final Answer:
The distance between the midpoints AD and BC is 5cm.
We have triangle ABC with:
- AB=8cm
- CD=6cm (the altitude from C to AB)
We can place the triangle in a coordinate system for easier calculations:
- Let A(0,0) and B(8,0) (since AB = 8 cm lies on the x-axis).
- Point C will be directly above the midpoint of AB since CD is the altitude. The midpoint M of AB is at (4,0).
- Since CD is vertical and has a length of 6 cm, the coordinates of point C will be C(4,6).
- Midpoint of AD (let's call it M1):
- A is at (0,0) and D is at (4,0) (the foot of the altitude).
- The midpoint M1 is calculated as:
M1=(0+42,0+02)=(2,0)
- B is at (8,0) and C is at (4,6).
- The midpoint M2 is calculated as:
M2=(8+42,0+62)=(6,3)
- The distance d between the points M1 and M2 can be calculated using the distance formula:
d=√(x2−x1)2+(y2−y1)2
- Substituting the coordinates of M1 and M2:
d=√(6−2)2+(3−0)2=√42+32=√16+9=√25=5cm
The distance between the midpoints AD and BC is 5cm.
Topper's Solved these Questions
Similar Questions
ΔABC is an acute angled triangle. CD be the altitude through C. If AB=8,CD=6 , then the distance between the mid-points of AD and BC is
View SolutionLet ABC be an acute angled triangle and CD be the altitude through C. If AB = 8 cm and CD = 6 cm, then the distance between the midpoints AD and BC is :
View Solution
Knowledge Check
Let ABC be an acute-angled triangle and let D be the midpoint of BC. If AB = AD, then tan(B)/tan(C) equals
A√2B√3C2D3Let ABC be an acute-angled triangle and let D be the midpoint of BC. If AB = AD, then tan(B)/tan(C) equals
A√2B√3C2D3△ABC is a right angled at A and AD is the altitude to BC. If AB= 7 cm and AC = 24 cm. Find the ratio of AD is to AM if M is the mid-point of BC.
A25:41B32:41C336/625D625/336
ΔABC is an acute angle triangle. AD is perpendiculra on BC and DB = 3 CD. Find BC2-
View SolutionIn a triangle ABC, ∠BCA=90∘ and CD is perpendicular to AB. If AD = 4 cm and BD = 9 cm, then the value of DC will be
View SolutionIn given figure, ABC is a triangle right angled at B and BD⊥AC. If AD=4 cm and CD= 5 cm, then find BD and AB.
View SolutionABC is triangle right angled at B. If AB = 6 cm and BC= 8 cm, then what is the length of the circum- radius of the ΔABC ?
View SolutionQuadrilateral ABCD circumscribes a circle. If AB = 8 cm, BC = 7 cm and CD = 6 cm, then the length of AD is:
View Solution